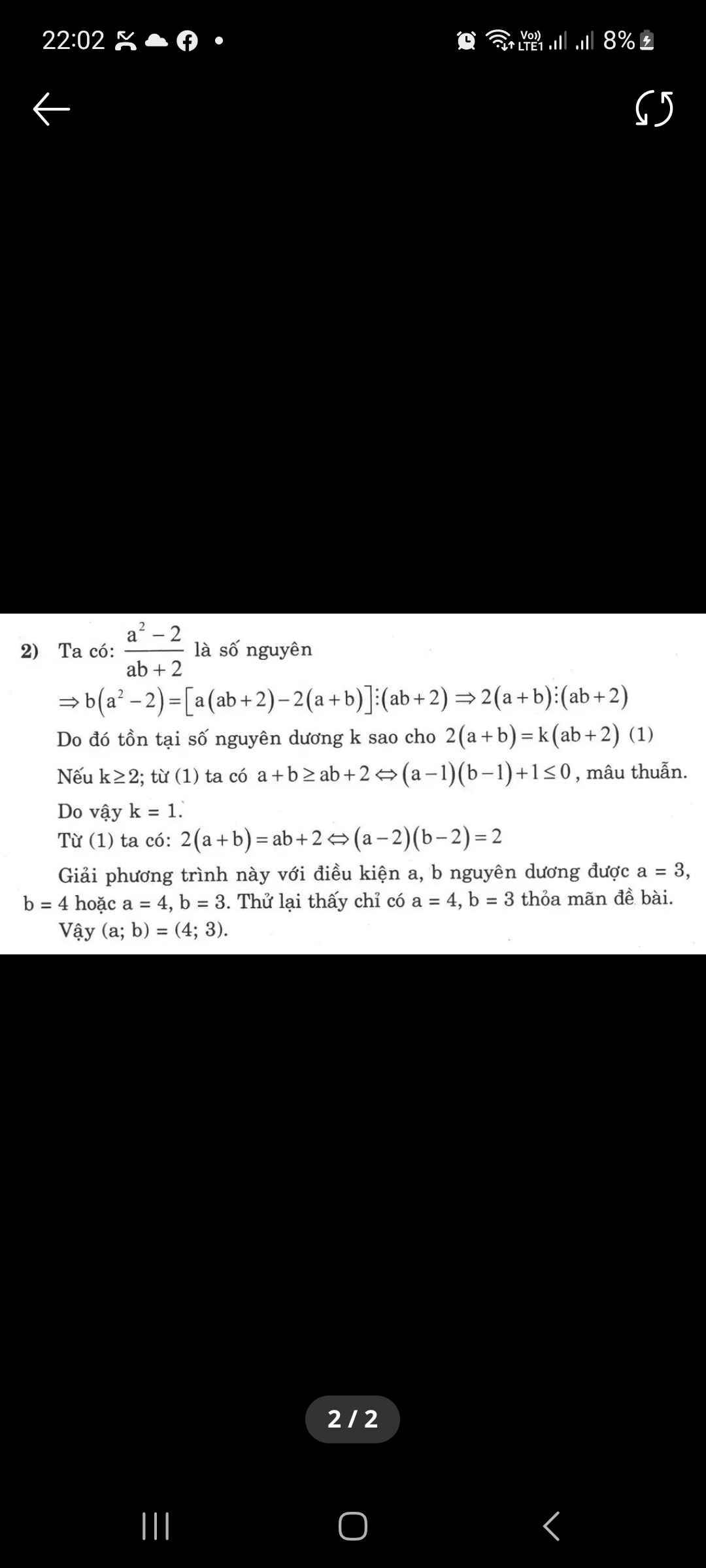Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu hỏi của NGUUYỄN NGỌC MINH - Toán lớp 9 - Học toán với OnlineMath

Đặt \(a-b=x;b-c=y;c-a=z\)
\(\Rightarrow x+y+z=a-b+b-c+c-a=0\)
Lúc đó: \(B=\frac{1}{x^2}+\frac{1}{y^2}+\frac{1}{z^2}\)
Mà \(x+y+z=0\Rightarrow2\left(x+y+z\right)=0\Rightarrow\frac{2\left(x+y+z\right)}{xyz}=0\)
\(\Rightarrow B=\frac{1}{x^2}+\frac{1}{y^2}+\frac{1}{z^2}+\frac{2\left(x+y+z\right)}{xyz}\)
\(=\frac{1}{x^2}+\frac{1}{y^2}+\frac{1}{z^2}+\frac{2}{yz}+\frac{2}{xz}+\frac{2}{xy}\)
\(=\left(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\right)^2\)

Ta có \(b\left(a^2-2\right)=a\left(ab+2\right)-2\left(a+b\right)\). Do \(a^2-2\vdots ab+2\) nên \(2\left(a+b\right)\vdots ab+2\to ab+2\le2a+2b\to\left(a-2\right)\left(b-2\right)\le2\).
Với \(a=1\to-\frac{1}{b+2}\in Z\), loại
Với \(a=2\to\frac{4}{2b+2}\in Z\to2b+2=4\to b=1\)
Với \(a=3\to\frac{7}{3b+2}\in Z\to3b+2=7\to\) loại
Với \(a=4\to\frac{14}{4b+2}\in Z\to4b+2=14\to b=3.\)
Với \(a\ge5\to b-2\le\frac{2}{a-2}<1\to b\le2\to b=1,2\). Với \(b=1\to\frac{a^2-2}{a+2}\in Z\to a-2+\frac{2}{a+2}\in Z\to a+2=2\to\) loại.
Nếu \(b=2\to\frac{a^2-2}{2a+2}\in Z\to\frac{a^2-2}{a+1}\in Z\to\frac{3}{a+1}\in Z\to a+1=3\to\) loại.
Vậy các cặp số \(\left(a,b\right)\) nguyên dương thoả mãn là \(\left(2,1\right);\left(4,3\right).\)

Đặt \(\left(\sqrt{a};\sqrt{b};\sqrt{c}\right)\rightarrow\left(x;y;z\right)\)\(\Rightarrow\)\(x^2+y^2+z^2=4\)
\(P=\frac{x^3}{x+3y}+\frac{y^3}{y+3z}+\frac{z^3}{z+3x}=\frac{x^4}{x^2+3xy}+\frac{y^4}{y^2+3yz}+\frac{z^4}{z^2+3zx}\)
\(\ge\frac{\left(x^2+y^2+z^2\right)^2}{x^2+y^2+z^2+3\left(xy+yz+zx\right)}\ge\frac{\left(x^2+y^2+z^2\right)^2}{x^2+y^2+z^2+3\left(x^2+y^2+z^2\right)}=\frac{4^2}{4+3.4}=1\)
Dấu "=" xảy ra \(\Leftrightarrow\)\(a=b=c=\frac{2}{\sqrt{3}}\)