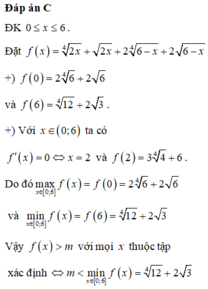
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
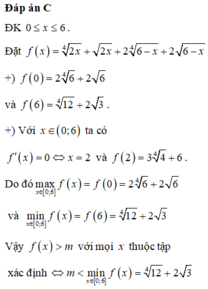
Đáp án A
Phương pháp: Chia cả 2 vế cho 3x, đặt 
, tìm điều kiện của t.
Đưa về bất phương trình dạng 
Cách giải :
Ta có 
Đặt 
, khi đó phương trình trở thành
Ta có: 
Vậy 
Đáp án A
Tập xác định của hàm số: D = 0 ; 4
Ø Xét tử số, đặt g x = x x + x + 12
Em thấy g x > 0 ∀ x ∈ 0 ; 4 g ' x = 3 x 2 x + 1 2 x + 12 > 0 ⇒ g x là hàm dương và đồng biến trên [0;4]
Ø Xét mẫu số, xét h x = 5 − x + 4 − x
Em thấy h x > 0 ∀ x ∈ 0 ; 4 h ' x = − 1 2 5 − x + − 1 2 4 − x < 0
=> h(x) là hàm dương và nghịch biến trên [0;4]
=> 1 h x là hàm đồng biến trên [0;4] ⇒ y = g x . 1 h x là hàm đồng biến trên [0;4]
⇒ maxy = y 4 = 12 ; miny = y 0 = 2 15 − 4 3
Câu 1:
\(\frac{1}{3}+\frac{3}{35}<\frac{x}{210}<\frac{4}{7}+\frac{3}{5}+\frac{1}{3}\)
\(\Rightarrow\frac{44}{105}<\frac{x}{210}<\frac{158}{105}\)
\(\Rightarrow\frac{88}{210}<\frac{x}{210}<\frac{316}{210}\)
\(\Rightarrow x\in\left\{89;90;91;92;...;310;311;312;313;314;315\right\}\)
Câu 3:
\(\frac{5}{3}\)\(+\frac{-14}{3}\)\(<\)\(x\)\(<\)\(\frac{8}{5}+\frac{18}{10}\)
\(\Rightarrow\)\(-9\)\(<\)\(x\)\(<\)\(3,4\)
Mà \(x\in Z\)
\(\Rightarrow x\in\left\{-8;-7;-6;-5;...;1;2;3\right\}\)