Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Phương trình đã cho tương đương với:
\(x^3-3x^2=m\)
Khảo sát và lập bẳng biến thiên hàm số vế trái ta có:
\(y=x^3-3x^2\)
Đạo hàm: \(y'=3x^2-6x\)
\(y'=0\Leftrightarrow x=0,x=2\)
Lập bảng biến thiên:
x y' y 0 2 0 0 + + - 8 8 + 8 + - 8 > > > 0 -4
Nhìn vào bảng biến thiên ta thấy để phương trình \(x^3-3x^2=m\) có 3 nghiệm phân biệt thì: \(-4< m< 0\)
Đáp án B
Đặt t = 2x > 1
PT
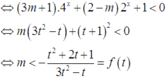
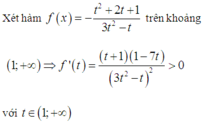
Dựa vào bảng biến thiên, suy ra m < -2
.
.
.
.
Đáp án C
Điều kiện của phương trình 
là 
hay 
Với điều kiện đó 
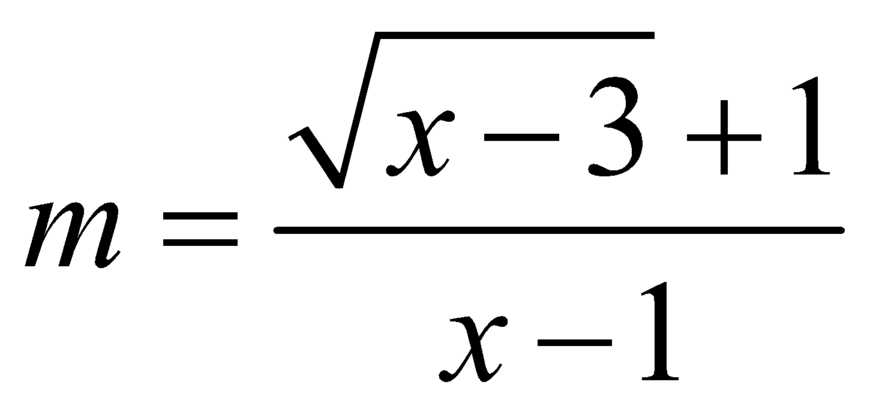
Xét hàm số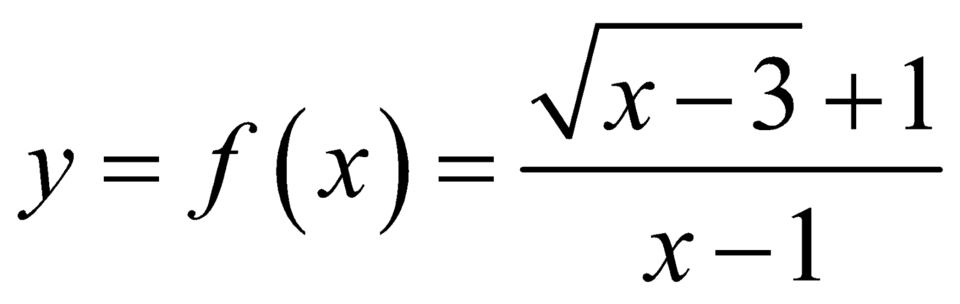 
với 
.
Trên 
, ta có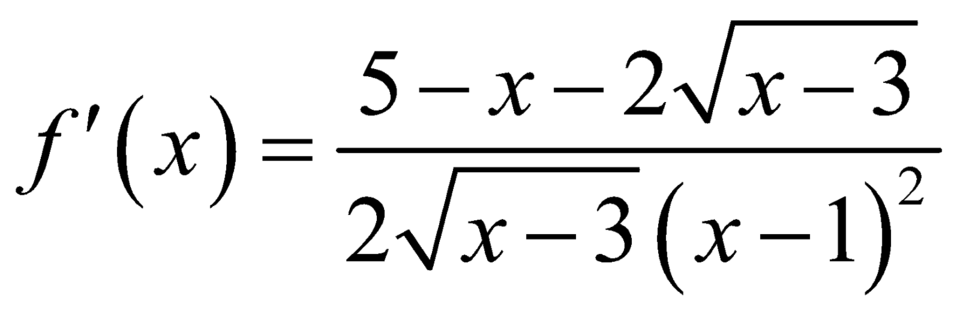 
,
.
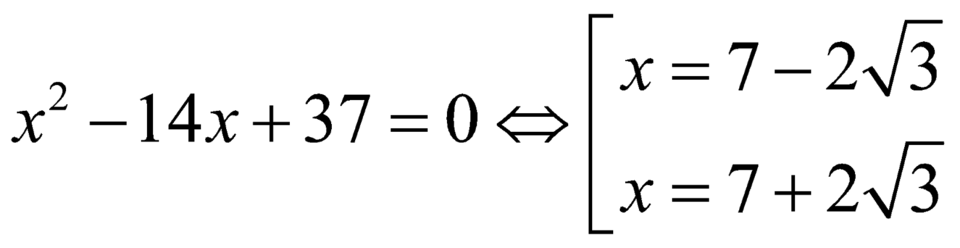Chỉ có giá trị 
thỏa.
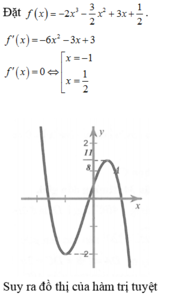
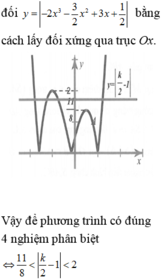
Vẽ đồ thị, ta thấy với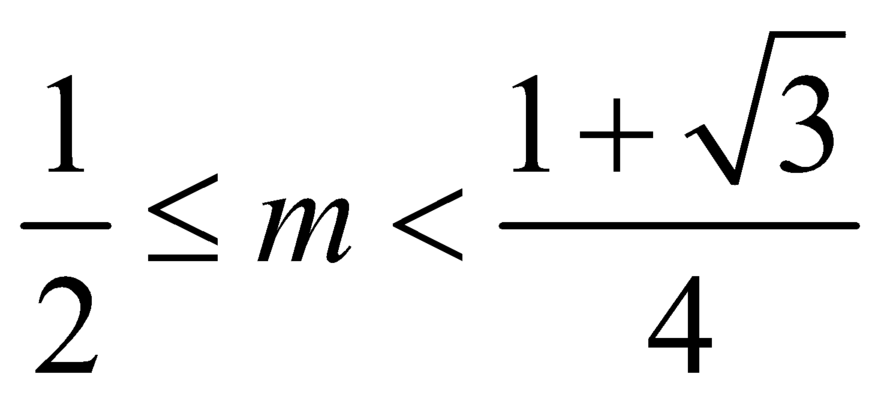 
thì đường thẳng y=m cắt đồ thị hàm số 
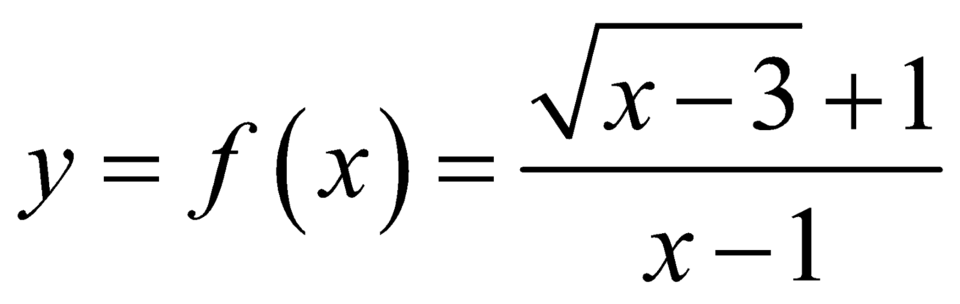tại hai điểm phân biệt.
Vậy phương trình 
có hai nghiệm phân biệt khi và chỉ khi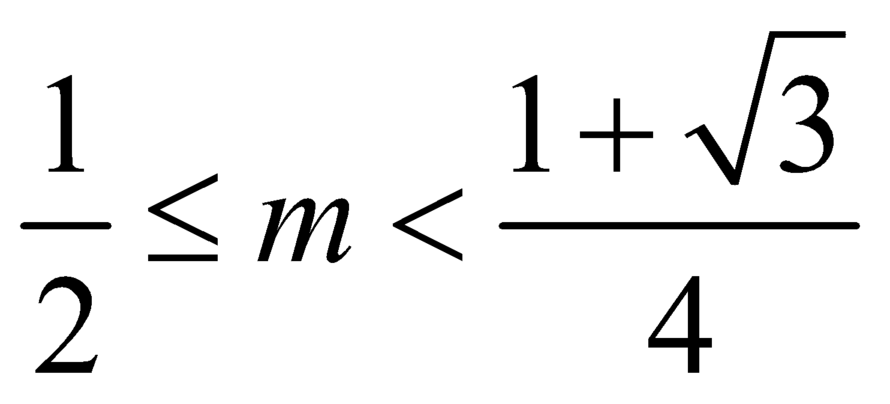 
.
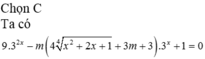
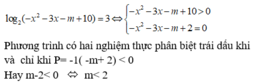
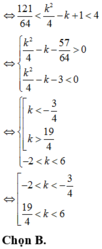
\(\Leftrightarrow x^3-3x^2-1=-3m\)
Xét hàm \(f\left(x\right)=x^3-3x^2-1\Rightarrow f'\left(x\right)=3x^2-6x=0\Rightarrow\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)
BBT:
Từ BBT ta thấy để đường thẳng \(y=-3m\) cắt đồ thị \(f\left(x\right)\) tại 3 điểm pb trong đó có đúng 2 điểm có hoành độ lớn hơn 1 \(\Leftrightarrow-5< -3m< -3\)
\(\Leftrightarrow1< m< \frac{5}{3}\)