Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có \(\sqrt{\left(m+2\right)x+m}\ge\left|x-1\right|\Leftrightarrow\left(m+2\right)x+m\ge x^2-2x+1\)
\(\Leftrightarrow m\ge\frac{x^2-4x+1}{x+1}\) (vì \(x\in\left[0;2\right]\)
Xét hàm số \(f\left(x\right)=\frac{x^2-4x+1}{x+1}\) trên đoạn \(\left[0;2\right]\) ta có
\(f'\left(x\right)=\frac{x^2+2x-5}{\left(x+1\right)^2};f'\left(x\right)=0\Leftrightarrow x=-1+\sqrt{6}\)
Lập bảng biến thiên ta được
\(f\left(0\right)=1;f\left(2\right)=-1\)
\(f\left(-1+\sqrt{6}\right)=2\sqrt{6}-6\)
Vậy bất phương trình đã cho có nghiệm thì \(m>\) min (0;2] \(f\left(x\right)=f\left(-1+\sqrt{6}\right)=2\sqrt{6-6}\)

Đáp án C
Điều kiện của phương trình ![]()
![]() là
là ![]() hay
hay ![]()
Với điều kiện đó ![]()
![]()
![]()
![]()
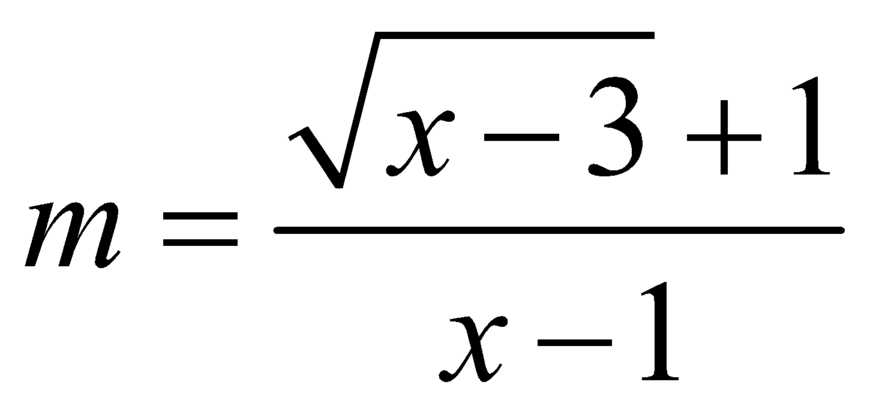
Xét hàm số 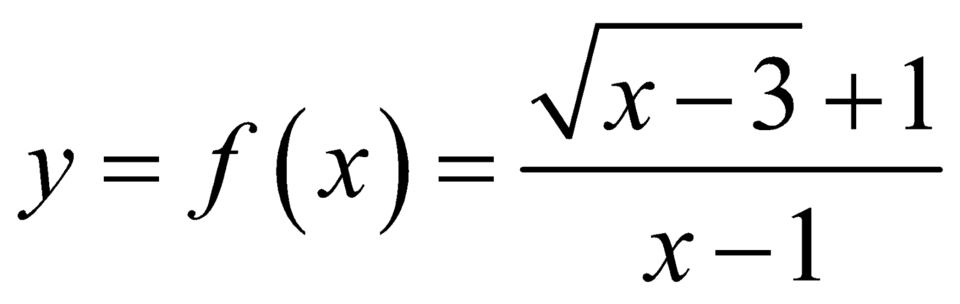 với
với ![]() .
.
Trên ![]() , ta có
, ta có 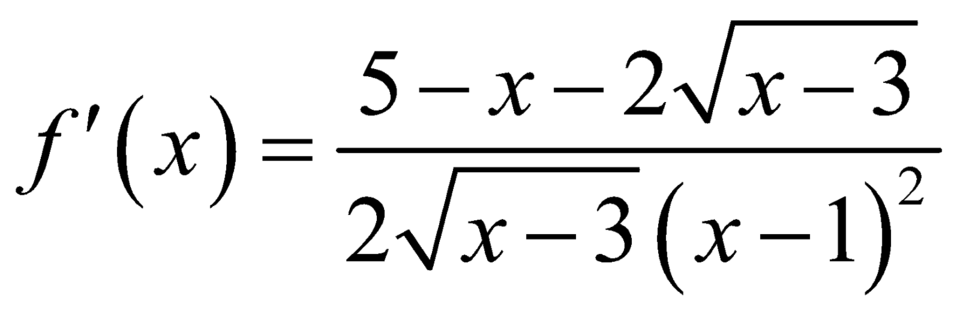 ,
,
![]()
![]()
![]()
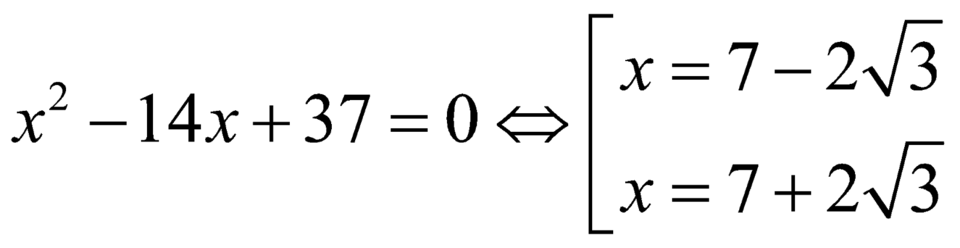 .
.
Chỉ có giá trị ![]() thỏa.
thỏa.
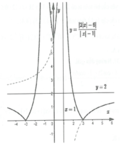
Vẽ đồ thị, ta thấy với 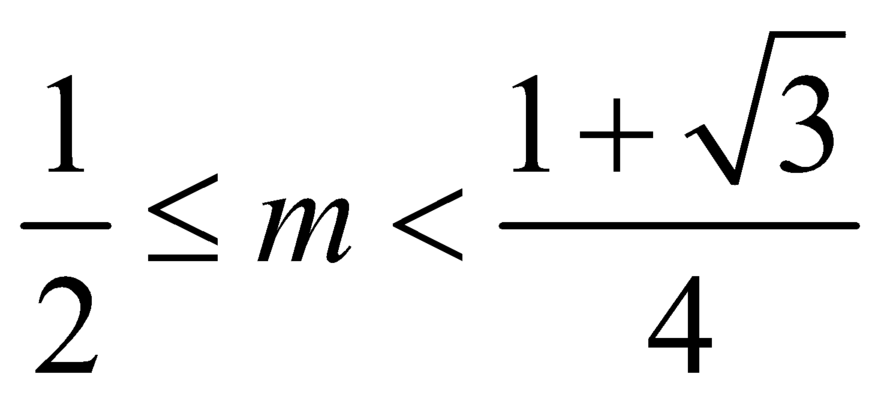 thì đường thẳng y=m cắt đồ thị hàm số
thì đường thẳng y=m cắt đồ thị hàm số 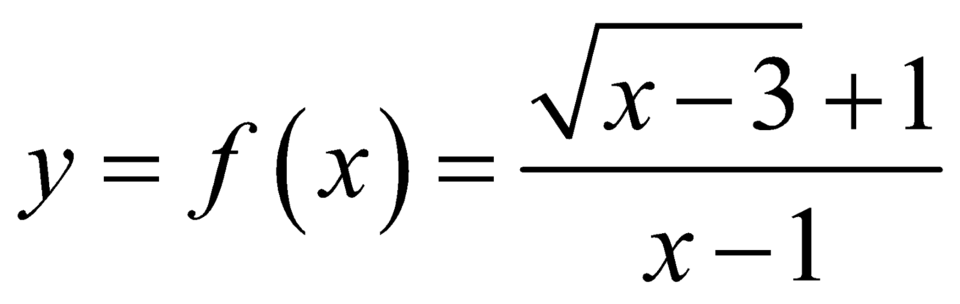 tại hai điểm phân biệt.
tại hai điểm phân biệt.
Vậy phương trình ![]() có hai nghiệm phân biệt khi và chỉ khi
có hai nghiệm phân biệt khi và chỉ khi 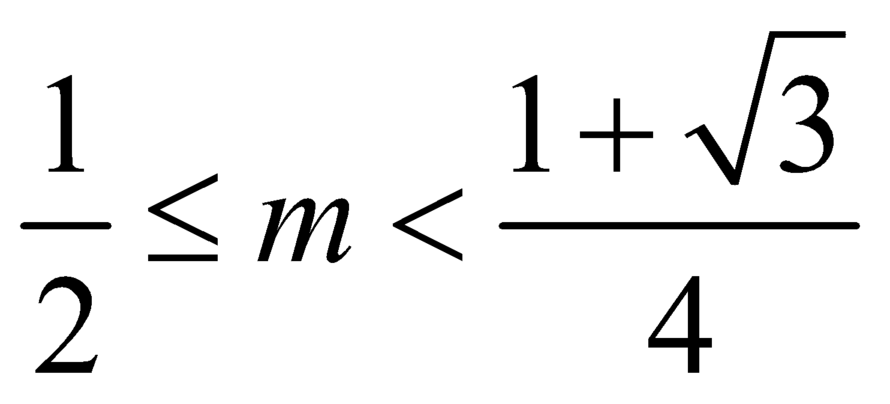 .
.

Điều kiện: x≥ -1/2
Phương trình
x 2 + m x + 2 = 2 x + 1 ⇔ 3 x 2 + 4 x - 1 = m x ( * )
Vì x= 0 không là nghiệm nên (*)
⇔ m = 3 x 2 + 4 x - 1 x
xét f ( x ) = 3 x 2 + 4 x - 1 x .
Ta có đạo hàm
f ' ( x ) = 3 x 2 + 1 x 2 > 0 ∀ x ⩾ - 1 2 ; x ≠ 0
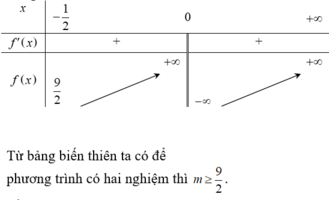
Bảng biến thiên
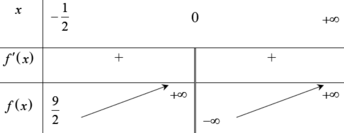
Từ bảng biến thiên ta có để phương trình có hai nghiệm thì m ≥ 9/2.
Chọn D.

Điều kiện: x ≥ - 1 2
Phương trình x 2 + m x + 2 = 2 x + 1 ⇔ 3 x 2 + 4 x - 1 = m x ( * )
Vì x=0 không là nghiệm nên (*) ⇔ m = 3 x 2 + 4 x - 1 x
Xét
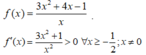
Bảng biến thiên
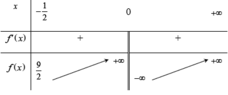
Từ bảng biến thiên ta có để phương trình có hai nghiệm thì m ≥ 9 2 .
Chọn C.






ĐKXĐ: \(x\ge3\)
\(\Leftrightarrow mx-\sqrt{x-3}=m+1\Leftrightarrow m\left(x-1\right)=\sqrt{x-3}+1\)
\(\Leftrightarrow m=\frac{\sqrt{x-3}+1}{x-1}\)
Đặt \(\sqrt{x-3}=t\ge0\) \(\Rightarrow x=t^2+3\Rightarrow m=\frac{t+1}{t^2+2}\)
Xét hàm \(f\left(t\right)=\frac{t+1}{t^2+2}\Rightarrow f'\left(t\right)=\frac{t^2+2-2t\left(t+1\right)}{\left(t^2+2\right)^2}=\frac{-t^2-2t+2}{\left(t^2+2\right)^2}\)
\(f'\left(t\right)=0\Rightarrow t=\sqrt{3}-1\)
Ta có \(f\left(\sqrt{3}-1\right)=\frac{1+\sqrt{3}}{4}\); \(\lim\limits_{t\rightarrow+\infty}\frac{t+1}{t^2+1}=0\); \(f\left(0\right)=\frac{1}{2}\)
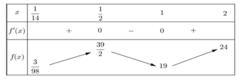
Dựa vào BBT, để pt đã cho có 2 nghiệm pb thì \(\frac{1}{2}\le m< \frac{1+\sqrt{3}}{4}\)