Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D.
Đặt t = 3x > 0, phương trình trở thành t2 - (m - 1) t + 2m = 0 (*)
Yêu cầu bài toán thành phương trình (*) có đúng một nghiệm dương.
+ (*) có nghiệm kép dương 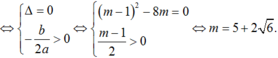
+ (*) có hai nghiệm trái dấu khi đó; 2m < 0 hay m < 0.
Vậy m < 0 hoặc ![]() thỏa yêu cầu bài toán.
thỏa yêu cầu bài toán.

Ta có \(\sqrt{\left(m+2\right)x+m}\ge\left|x-1\right|\Leftrightarrow\left(m+2\right)x+m\ge x^2-2x+1\)
\(\Leftrightarrow m\ge\frac{x^2-4x+1}{x+1}\) (vì \(x\in\left[0;2\right]\)
Xét hàm số \(f\left(x\right)=\frac{x^2-4x+1}{x+1}\) trên đoạn \(\left[0;2\right]\) ta có
\(f'\left(x\right)=\frac{x^2+2x-5}{\left(x+1\right)^2};f'\left(x\right)=0\Leftrightarrow x=-1+\sqrt{6}\)
Lập bảng biến thiên ta được
\(f\left(0\right)=1;f\left(2\right)=-1\)
\(f\left(-1+\sqrt{6}\right)=2\sqrt{6}-6\)
Vậy bất phương trình đã cho có nghiệm thì \(m>\) min (0;2] \(f\left(x\right)=f\left(-1+\sqrt{6}\right)=2\sqrt{6-6}\)

Phương trình hoành độ giao điểm : \(-x^4+2\left(2+m\right)x^2-3-2m=0\left(1\right)\)
Đặt \(t=x^2,\left(t\ge0\right)\), phương trình (1) trở thành : \(t^2-1\left(m+2\right)t+3+2m=0\left(2\right)\)
(1) có 4 nghiệm phân biệt khi và chỉ khi (2) có 2 nghiệm dương phân biệt
Điều kiện là : \(\begin{cases}\Delta'>0\\S>0\\P>0\end{cases}\) \(\Leftrightarrow\begin{cases}m^2+2m+1>0\\m+2>0\\3+2>0\end{cases}\) \(\Leftrightarrow\begin{cases}m\ne-1\\m>-\frac{3}{2}\end{cases}\) (*)
Với điều kiện (*), giả sử \(t_1;t_2\) (\(0 < t 1 < t2 \) là 2 nghiệm phân biệt của (2), khi đó (1) có 4 nghiệm phân biệt là \(x_1=-\sqrt{t_2};x_2=-\sqrt{t_1};x_3=\sqrt{t_1};x_4=\sqrt{t_2};\)
\(x_1;x_2;x_3;x_4\) lập thành một cấp số cộng khi và chỉ khi :
\(x_2-x_1=x_3-x_2=x_4-x_3\)
\(\Leftrightarrow t_2=9t_1\left(a\right)\)
Áp dụng định lí Viet ta có : \(t_1+t_2=2\left(m+2\right);t_1.t_2=3+2m\left(b\right)\)
Từ (a) và (b) ta có : \(9m^2-14m-39=0\)
Đối chiếu điều kiện (*) ta có \(m=3\) hoặc \(m=-\frac{13}{9}\)

Đặt \(4^x=t>0\) pt trở thành:
\(f\left(t\right)=\left(m+1\right)t^2-2\left(2m-3\right)t+6m+5=0\) (1)
Để pt đã cho có 2 nghiệm trái dấu thì (1) cần có 2 nghiệm phân biệt thỏa mãn:
\(0< t_1< 1< t_2\) \(\Rightarrow\left\{{}\begin{matrix}a.f\left(0\right)>0\\a.f\left(1\right)< 0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}\left(m+1\right)\left(6m+5\right)>0\\\left(m+1\right)\left(3m+12\right)< 0\end{matrix}\right.\)
\(\Rightarrow-4< m< -1\) \(\Rightarrow a.b=\left(-1\right).\left(-4\right)=4\)

Đặt \(\left|cosx\right|=a\Rightarrow0\le a\le1\)
Phương trình trở thành \(\frac{1}{3}a^3-3a^2+5a-3+2m=0\) (1)
Để phương trình ban đầu có đúng 4 nghiệm pb thuộc \(\left[0;2\pi\right]\) \(\Leftrightarrow\left(1\right)\) có nghiệm duy nhất thuộc \(\left(0;1\right)\)
Xét \(f\left(a\right)=\frac{1}{3}a^3-3a^2+5a-3\)
\(f'\left(a\right)=a^2-6a+5=0\Rightarrow\left[{}\begin{matrix}a=1\\a=5\end{matrix}\right.\) \(\Rightarrow f\left(a\right)\) đồng biến trên \(\left(0;1\right)\)
\(f\left(0\right)=-3\); \(f\left(1\right)=-\frac{2}{3}\)
\(\Rightarrow-3< -2m< -\frac{2}{3}\Rightarrow\frac{1}{3}< m< \frac{3}{2}\)

Đặt \(3^x=t>0\) pt trở thành \(t^2-\left(m-1\right)t+2m=0\) (1)
Ta nhận thấy với mỗi giá trị dương của t sẽ cho 1 giá trị x tương ứng, do đó để pt đã cho có nghiệm duy nhất \(\Rightarrow\left(1\right)\) có nghiệm kép dương hoặc có 1 nghiệm dương, 1 nghiệm không dương
\(\Rightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}\Delta=0\\-\dfrac{b}{2a}>0\end{matrix}\right.\\a.c< 0\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}m^2-10m+1=0\\m>1\end{matrix}\right.\\2m< 0\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}m=5+2\sqrt{6}\\m< 0\end{matrix}\right.\)