SG
7
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
SG
1
SG
4
H
20 tháng 4 2017
Giải:
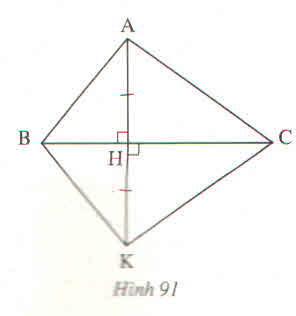
∆AHB và ∆KBH có
AH=KH(gt)
\(\widehat{AHB}\)=\(\widehat{KHM}\)
BH cạnh chung .
nên ∆AHB=∆KBH(c.g.c)
suy ra: \(\widehat{ABH}\)=\(\widehat{KBH}\)
Vậy BH là tia phân giác của góc B.
Tương tự ∆AHC =∆KHC(c.g.c)
Suy ra: \(\widehat{ACH}\)=\(\widehat{KCH}\)
Vậy CH là tia phân giác của góc C.
SG
1
H
20 tháng 4 2017
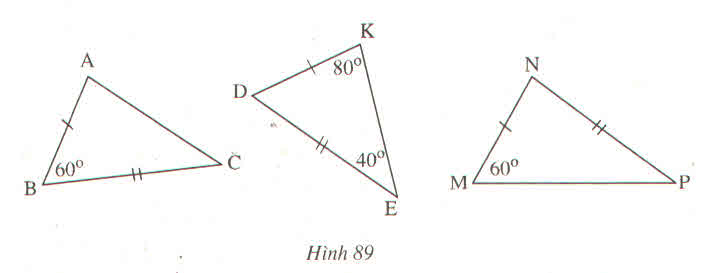
Tam giác DKE có:
\(\widehat{D}+\widehat{K}+\widehat{E}\)=1800 (tổng ba góc trong của tam giác).
\(\widehat{D}\)+800 +400=1800
\(\widehat{D}\)=1800 -1200= \(60^0\)
Nên ∆ ABC và ∆KDE có:
AB=KD(gt)
\(\widehat{B}\)=\(\widehat{D}\)=600và BE= ED(gt)
Do đó ∆ABC= ∆KDE(c.g.c)
Tam giác MNP không có góc xem giữa hai cạnh tam giác KDE ha ABC nên không bằng hai tam giác còn lại.
2 tháng 6 2017
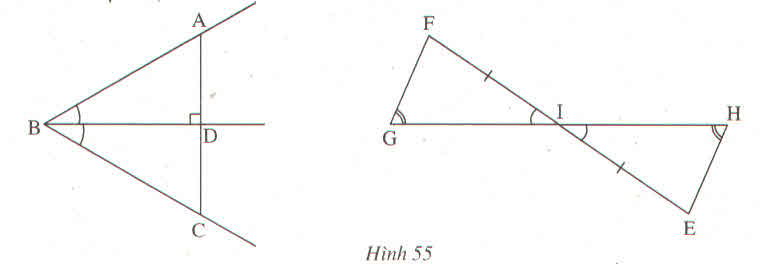
-Xét tam giác vuông BDA và tam giác vuông BDC có:
ABD = CBD
BD: cạnh chung
=> tam giác BDA = tam giác BDC
-Ta có: góc G = góc H
góc FIG = góc EIH
Mà F + G + FIG = E + H + EIH = 1800
=> góc F = góc E
Xét tam giác IFG và tam giác IEH có:
IF = IE (gt)
FIG = EIH (gt)
góc F = góc E (cmt)
=> tam giác IFG = tam giác IEH
SG
2
QD
20 tháng 4 2017
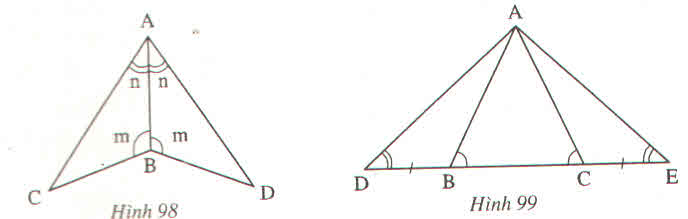
- Xem hình 98
∆ABC và ∆ABD có:
∠CAB = ∠DAB(gt)
AB là cạnh chung.
∠CBA = ∠DBA (gt)
Nên ∆ABC=∆ABD(g.c.g)
- Xem hình 99.
Ta có:
∠ABC + ∠ABD =1800 (Hai góc kề bù).
∠ACB + ∠ACE =1800
Mà ∠ABC = ∠ACB(gt)
Nên ∠ABD = ∠ACE
* ∆ABD và ∆ACE có:
∠ABD = ∠ACE (cmt)
BD=EC(gt)
∠ADB = ∠AEC (gt)
Nên ∆ABD=∆ACE(g.c.g)
* ∆ADC và ∆AEB có:
∠ADC = ∠AEB (gt)
∠ACD = ∠ABE (gt)
Ta có: DC = DB + BC
EB = EC + BC
Mà BD = EC (gt)
⇒ DC = EB
Nên ∆ADC=∆AEB(g.c.g)
SG
4
13 tháng 5 2017
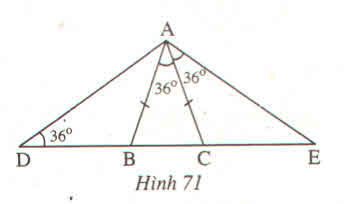
Tam giác ABC có AB = AC (theo đề bài)
Suy ra: tam giác ABC cân tại A( dựa theo định nghĩa tam giác cân)
=> góc ABC = góc ACB ( dựa theo tính chất tam giác cân)
=> góc ABC = góc ACB = \(\left(180^0-36^0\right):2=72^0\)
Có góc ACB + góc ACE = \(180^0\) (2 góc kề bù)
=> góc ACE = \(180^0\)- góc ACB
=> góc ACE = \(180^0-72^0=108^0\)
Tam giác ACE có góc CAE + góc CEA + góc ACE = \(180^0\)(tổng 3 góc của 1 tam giác)
=> góc CEA = \(180^0-\left(108^0+36^0\right)=36^0\)(*)
Tam giác ADE có góc BDA = góc CEA = \(36^0\)
=> tam giác ADE cân tại A ( dựa theo tính chất của tam giác cân)
Ta có: ∆AMD=∆AME(Cạnh huyền AM chung, góc nhọn^A1 = ^A2)
∆MDB=∆MEC(Cạnh huyền BM=CM, cạnh góc vuông.
MD=ME, do ∆AMD=∆AME)
∆AMB= ∆AMC(Cạnh AM chung),
Cạnh MB=MC, cạnh AB=AC
Vì AD=AE, DB=EC
Ta có: \(\Delta\)AMD=\(\Delta\)AME(Cạnh huyền AM chung, góc nhọn \(\widehat{A}_1=\widehat{A}_2\))
\(\Delta\)MDB=\(\Delta\)MEC(Cạnh huyền BM=CM, cạnh góc vuông )
MD=ME, do \(\Delta\)AMD=\(\Delta\)AME)
\(\Delta\)AMB= \(\Delta\)AMC(Cạnh AM chung),
Cạnh MB=MC, cạnh AB=AC
Vì AD=AE, DB=EC