Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\dfrac{\sqrt{x}+1}{\sqrt{x}-3}=\dfrac{\sqrt{x}-3+4}{\sqrt{x}-3}=1+\dfrac{4}{\sqrt{x}-3}\)
Để biểu thức đã cho nhận giá trị nguyên buộc \(\dfrac{4}{\sqrt{x}-3}\) nguyên
\(\Rightarrow\sqrt{x}-3\inƯ\left(4\right)\in\left\{-4;-2;-1;1;2;4\right\}\)
\(\Rightarrow x\in\left\{1;4;16;25;49\right\}\)
Vậy ......

a) \(P\)\(=\sqrt{x}-2+3-3\sqrt{x}=1-2\sqrt{x}\)
b) \(Q=\frac{2\left(1-2\sqrt{x}\right)}{1-1+2\sqrt{x}}=\frac{1-2\sqrt{x}}{\sqrt{x}}=\frac{1}{\sqrt{x}}-2\)
vậy x=1 thỏa mãn đề bài.
Trả lời :.............................
x=1...........................
Hk tốt..............................

1) \(ĐKXĐ:\hept{\begin{cases}x\ge0\\x\ne4\end{cases}}\)
\(P=\frac{2+\sqrt{x}}{2-\sqrt{x}}-\frac{2-\sqrt{x}}{2+\sqrt{x}}-\frac{4x}{x-4}\)
\(\Leftrightarrow P=\frac{\left(2+\sqrt{x}\right)^2-\left(2-\sqrt{x}\right)^2+4x}{\left(2+\sqrt{x}\right)\left(2-\sqrt{x}\right)}\)
\(\Leftrightarrow P=\frac{4+4\sqrt{x}+x-4+4\sqrt{x}-x+4x}{\left(2+\sqrt{x}\right)\left(2-\sqrt{x}\right)}\)
\(\Leftrightarrow P=\frac{4x+8\sqrt{x}}{\left(2+\sqrt{x}\right)\left(2-\sqrt{x}\right)}\)
\(\Leftrightarrow P=\frac{4\sqrt{x}}{2-\sqrt{x}}\)
2) Để \(P=2\)
\(\Leftrightarrow\frac{4\sqrt{x}}{2-\sqrt{x}}=2\)
\(\Leftrightarrow4\sqrt{x}=4-2\sqrt{x}\)
\(\Leftrightarrow6\sqrt{x}=4\)
\(\Leftrightarrow\sqrt{x}=\frac{2}{3}\)
\(\Leftrightarrow x=\frac{4}{9}\)
Vậy để \(P=2\Leftrightarrow x=\frac{4}{9}\)
3) Khi \(\left(\sqrt{x}-2\right)\left(2\sqrt{x}-1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}\sqrt{x}-2=0\\2\sqrt{x}-1==0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}\sqrt{x}=2\\\sqrt{x}=\frac{1}{2}\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=4\left(ktm\right)\\x=\frac{1}{4}\left(tm\right)\end{cases}}\)
Thay \(x=\frac{1}{4}\)vào P, ta được :
\(\Leftrightarrow P=\frac{4\sqrt{\frac{1}{4}}}{2-\sqrt{\frac{1}{4}}}=\frac{4\cdot\frac{1}{2}}{2-\frac{1}{2}}=\frac{2}{\frac{3}{2}}=\frac{4}{3}\)
4) Để \(P=\frac{\sqrt{x}+3}{2\sqrt{x}-1}\)
\(\Leftrightarrow\frac{4\sqrt{x}}{2-\sqrt{x}}=\frac{\sqrt{x}+3}{2\sqrt{x}-1}\)
\(\Leftrightarrow8x-4\sqrt{x}=-x-\sqrt{x}+6\)
\(\Leftrightarrow9x-3\sqrt{x}-6=0\)
\(\Leftrightarrow3x-\sqrt{x}-2=0\)
\(\Leftrightarrow\sqrt{x}=3x-2\)
\(\Leftrightarrow x=9x^2-12x+4\)
\(\Leftrightarrow9x^2-13x+4=0\)
\(\Leftrightarrow\left(9x-4\right)\left(x-1\right)=0\)
\(\Leftrightarrow\hept{\begin{cases}9x-4=0\\x-1=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=\frac{4}{9}\\x=1\end{cases}}\)
Thử lại ta được kết quá : \(x=\frac{4}{9}\left(ktm\right)\); \(x=1\left(tm\right)\)
Vậy để \(P=\frac{\sqrt{x}+3}{2\sqrt{x}-1}\Leftrightarrow x=1\)
5) Để biểu thức nhận giá trị nguyên
\(\Leftrightarrow\frac{4\sqrt{x}}{2-\sqrt{x}}\inℤ\)
\(\Leftrightarrow4\sqrt{x}⋮2-\sqrt{x}\)
\(\Leftrightarrow-4\left(2-\sqrt{x}\right)+8⋮2-\sqrt{x}\)
\(\Leftrightarrow8⋮2-\sqrt{x}\)
\(\Leftrightarrow2-\sqrt{x}\inƯ\left(8\right)=\left\{\pm1;\pm2;\pm4;\pm8\right\}\)
\(\Leftrightarrow\sqrt{x}\in\left\{1;3;0;4;-2;6;-6;10\right\}\)
Ta loại các giá trị < 0
\(\Leftrightarrow\sqrt{x}\in\left\{1;3;0;4;6;10\right\}\)
\(\Leftrightarrow x\in\left\{1;9;0;16;36;100\right\}\)
Vậy để \(P\inℤ\Leftrightarrow x\in\left\{1;9;0;16;36;100\right\}\)
\(\)

\(A=\frac{\sqrt{x}-1}{\sqrt{x}+1}=\frac{\sqrt{x}+1-2}{\sqrt{x}+1}=1-\frac{2}{\sqrt{x}+1}\)
vì x nguyên để A nhận GT nguyên thì \(\frac{2}{\sqrt{x}+1}\in Z\)\(\Rightarrow2⋮\sqrt{x}+1\)\(\Rightarrow\sqrt{x}+1\inƯ\left(2\right)=\left\{1;-1;2;-2\right\}\)
Mà \(\sqrt{x}+1\ge0+1=1\)nên \(\sqrt{x}+1\in\left\{1;2\right\}\Rightarrow\sqrt{x}\in\left\{0;1\right\}\)
\(\Rightarrow x\in\left\{0;1\right\}\)
Đây là bài của lớp 7 mà
Ta có \(A=\frac{\sqrt{x}-1}{\sqrt{x}+1}=\frac{\sqrt{x}+1-2}{\sqrt{x}+1}=1-\frac{2}{\sqrt{x}+1}\)
Vì \(x\in Z\Rightarrow\sqrt{x}\in Z\)
Để \(A\in Z\Rightarrow\frac{2}{\sqrt{x}+1}\in Z\)
\(\Rightarrow\sqrt{x}+1\inƯ\left(2\right)=\left\{-2;-1;1;2\right\}\)
Mà \(\sqrt{x}\ge0\) \(\forall x\)
\(\Rightarrow\sqrt{x}+1\ge1\)
\(\Rightarrow\orbr{\begin{cases}\sqrt{x}+1=1\\\sqrt{x}+1=2\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}\sqrt{x}=0\\\sqrt{x}=1\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}x=0\\x=1;x=-1\end{cases}}\)
Vậy \(x\in\left\{0;1;-1\right\}\)

a ) \(ĐKXĐ:x\ge0;x\ne1\)
= \(\frac{x+1+\sqrt{x}}{x+1}:\left[\frac{1}{\sqrt{x}-1}-\frac{2\sqrt{x}}{\left(x+1\right)\left(\sqrt{x}-1\right)}\right]-1\)
\(=\frac{x+1+\sqrt{x}}{x+1}:\frac{x+1-2\sqrt{x}}{\left(x+1\right)\left(\sqrt{x}-1\right)}-1\)
\(=\frac{x+1+\sqrt{x}}{x+1}:\frac{\left(\sqrt{x}-1\right)^2}{\left(x+1\right)\left(\sqrt{x}-1\right)}-1\)
\(=\frac{\left(x+1+\sqrt{x}\right)\left(x+1\right)\left(\sqrt{x}-1\right)}{\left(x+1\right)\left(\sqrt{x}-1\right)^2}-1\)
\(=\frac{x+1+\sqrt{x}}{\sqrt{x}-1}-1=\frac{x+2}{\sqrt{x}-1}\)
B ) Ta có :
\(Q=P-\sqrt{x}\)
\(=\frac{\sqrt{x}+2}{\sqrt{x}-1}-\sqrt{x}\)
\(=\frac{\sqrt{x}+2}{\sqrt{x}-1}=\frac{\left(\sqrt{x}-1\right)+3}{\sqrt{x}-1}=1+\frac{3}{\sqrt{x}-1}\)
Đế Q nhận giá trị nguyên thì \(1+\frac{3}{\sqrt{x}-1}\in Z\)
\(\Leftrightarrow\frac{3}{\sqrt{x}-1}\in Z\left(vì1\in Z\right)\)
\(\Leftrightarrow\sqrt{x}-1\inƯ\left(3\right)\)
Ta có bảng sau :
| \(\sqrt{x}-1\) | 3 | -3 | 1 | -1 |
| \(\sqrt{x}\) | 4 | -2 | 2 | 0 |
| \(x\) | 16(t/m) | 4(t/m) | 0(t/m) |
Vậy để biểu thức \(Q=P-\sqrt{x}\) nhận giá trị nguyên thì \(x\in\left\{16;4;0\right\}\)

bÀI LÀM
a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)

\(P=\frac{4\sqrt{x}+3}{x+\sqrt{x}}+\frac{\sqrt{x}}{\sqrt{x}+1}\)
\(P=\frac{4\sqrt{x}+3}{\sqrt{x}\left(\sqrt{x}+1\right)}+\frac{\sqrt{x}}{\sqrt{x}+1}=\frac{4\sqrt{x}+3}{\sqrt{x}\left(\sqrt{x}+1\right)}+\frac{x}{\sqrt{x}\left(\sqrt{x}+1\right)}\)
\(=\frac{x+4\sqrt{x}+3}{\sqrt{x}\left(\sqrt{x}+1\right)}\inℤ\Leftrightarrow x+4\sqrt{x}+3⋮\sqrt{x}\)
Giải tiếp nhé sau đó thử chọn :V
\(p=\frac{4\sqrt{x}+3}{x+\sqrt{x}}+\frac{\sqrt{x}}{\sqrt{x}+1}\)
\(=\frac{4\sqrt{x}+3}{\sqrt{x}\left(\sqrt{x}+1\right)}+\frac{x}{\sqrt{x}\left(\sqrt{x}+1\right)}\)
\(=\frac{x+\sqrt{x}+3\sqrt{x}+3}{\sqrt{x}\left(\sqrt{x}+1\right)}=\frac{\left(\sqrt{x}+3\right)\left(\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}+1\right)}\)
\(=\frac{\sqrt{x}+3}{\sqrt{x}}=1+\frac{3}{\sqrt{x}}\)
Để \(x\in Z\Rightarrow P\in Z\)
\(\Rightarrow\sqrt{x}\inƯ\left(3\right)= \left\{-3;3\right\}\)
\(\Leftrightarrow x=9\left(t.mĐKXĐ\right)\)


Ta có: x + 1 x - 3 = x - 3 + 4 x - 3 = 1 + 4 x - 3
Để 1 + 4 x - 3 nhận giá trị nguyên thì 4 x - 3 phải có giá trị nguyên. Vì x nguyên nên √x là số nguyên hoặc số vô tỉ.
* Nếu x là số vô tỉ thì x - 3 là số vô tỉ nên 4 x - 3 không có giá trị nguyên. Trường hợp này không có giá trị nào của x để biểu thức nhận giá trị nguyên.
* Nếu x là số nguyên thì x - 3 là số nguyên. Vậy để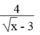 nguyên thì
x
- 3 phải là ước của 4.
nguyên thì
x
- 3 phải là ước của 4.
Đồng thời x ≥ 0 suy ra: x ≥ 0
Ta có: W(4) = {-4; -2; -1; 1; 2; 4}
Suy ra: x - 3 = -4 ⇒ x = -1 (loại)
x - 3 = -2 ⇒ x = 1 ⇒ x = 1
x - 3 = -1 ⇒ x = 2 ⇒ x = 4
x - 3 = 1 ⇒ x = 4 ⇒ x = 16
x - 3 = 2 ⇒ x = 5 ⇒ x = 25
x - 3 = 4 ⇒ x = 7 ⇒ x = 49
Vậy với x ∈ {1; 4; 16; 25; 49} thì biểu thức x + 1 x - 3 nhận giá trị nguyên.