Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Với câu c, Thiên Anh nên thêm điều kiện để phần kết luận là: \(0\le x< 2.\)

a) = 225
b) 49
c) = 1
d) 1 ; 2 ; 3 ; 4 ; 5 ; 6 ; 7
k nha
a) \(\sqrt{x}=15\)
=> x = 152
=> x = 225
b) \(2\sqrt{x}=14\)
<=> \(\sqrt{x}=7\)
=> x = 72
=> x = 49
c) \(\sqrt{x}< \sqrt{2}\)
<=> x < 2
mà \(x\ge0\)
=> x= {0;1}
d) \(\sqrt{2x}< 4\)
=> 2x < 16
<=> x < 8
mà \(x\ge0\)
=> x = {0;1;2;3;4;5;6;7}
ok mk nhé!!!!!! 53654645756876969251353253434645655435436464556756252345345634

a)\(\sqrt{x}>2\Leftrightarrow\sqrt{x^2}>2^2\Leftrightarrow x>4\)
\(\sqrt{x}< 1\Leftrightarrow\sqrt{x^2}< 1^2\Leftrightarrow x< 1\)

a) 225
b)17:2=7 =>x=47
c)căn 2=1,4142.... mà x ko âm thì dương nên x bằng 1
d)x chắc bằng 1
à lúc mình học lớp 6 hay 7 gì đó thì mấy câu này mình giải như vậy thôi

a: \(=4x-4x\sqrt{2}-2x\sqrt{2}+2x=6x-6x\sqrt{2}\)
b: \(=6x-4\sqrt{xy}+3\sqrt{xy}-2y=6x-\sqrt{xy}-2y\)

\(A=2x+\sqrt{4-2x^2}=\sqrt{2}.\sqrt{2x^2}+\sqrt{4-2x^2}\)
áp dụng BĐT bunhiacopxki,ta có:
\(A^2\le\left(2+1\right)\left(2x^2+4-2x^2\right)=3.4=12\)
\(\Leftrightarrow A\le\sqrt{12}\)
dấu = xảy ra khi \(\frac{\sqrt{2}}{\sqrt{2}x}=\frac{1}{\sqrt{4-2x^2}}\Leftrightarrow4-2x^2=x^2\Leftrightarrow x=\sqrt{\frac{4}{3}}=\frac{2}{\sqrt{3}}\)
vậy Amax = \(\sqrt{12}\)khi x=\(\frac{2}{\sqrt{3}}\)

\(\sqrt{x}=3\Rightarrow x=9\)
\(\sqrt{x}=\sqrt{5}\Rightarrow x=5\)
\(\sqrt{x}=0\Rightarrow x=0\)
\(\sqrt{x}=-2\Rightarrow x=\varnothing\)
a)\(\sqrt{x}=3\Rightarrow x=9\)
b)\(\sqrt{x}=\sqrt{5}\Rightarrow x=5\)
c)\(\sqrt{x}=0\Rightarrow x=0\)
d)\(\sqrt{x}=-2\Rightarrow x=4\)

2) \(a.\sqrt{\left(-15\right)^2}=\left|15\right|=15\)
\(b.\sqrt{\left(2-\sqrt{5}\right)^2}=\left|2-\sqrt{5}\right|=2-\sqrt{5}\)
\(c.\sqrt{\left(3-\sqrt{7}\right)^2}=\left|3-\sqrt{7}\right|=3-\sqrt{7}\)
\(d.2\sqrt{a^2}=\left|2\sqrt{a}\right|=2\sqrt{a}\)
bai1
a)
√x=5=> x=25
b)
√(x+1)=2; x+1=4;x=3
c)
√(x^2)=4=> x=±4; x>0=>x=4
d)
2√(x+1)=4=>√(x+1)=2
x+1=4;x=3
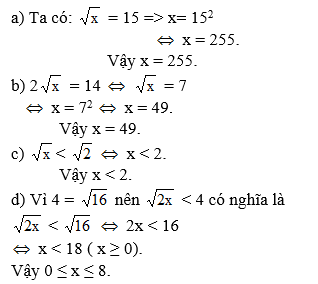
a/\(\sqrt{x}=7\)
\(\Leftrightarrow x=49\)
b/\(\Leftrightarrow x< 4\)(do x>0)
\(\Rightarrow x\varepsilon\left\{0;1;2;3\right\}\)
c/\(2x< 16\)
\(\Leftrightarrow x< 8\)
\(\Leftrightarrow x\varepsilon\left\{1;2;3;4;5;6;7\right\}\)
a) \(2\sqrt{x}=14\Leftrightarrow\sqrt{x}=7\)
\(\Leftrightarrow x=7^2\Leftrightarrow x=49\)
b) \(\sqrt{x}< \sqrt{2}\Leftrightarrow x< 2\)
c) \(\sqrt{2x}< 4\)
Vì \(4=\sqrt{16}\text{ nên }\sqrt{2x}< 4\text{ có nghĩa là }\sqrt{2x}< 16\)
\(\Leftrightarrow2x< 16\)
\(\Leftrightarrow x< 8\left(x\ge0\right)\)