Tìm số tự nhiên n để:a) n + 3 ⋮ n

Khách

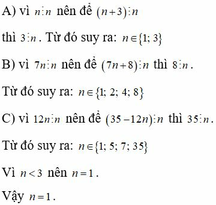
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mua vip

Pham Trong Bach

19 tháng 1 2018

Tìm số tự nhiên n để:

a) $(n + 3) ⋮ n$

b) $(7 n + 8) ⋮ n$

c) $(35 - 12 n) ⋮ n$ với n < 3

#Hỏi cộng đồng OLM #Toán lớp 6

Cao Minh Tâm

19 tháng 1 2018

Đúng(1)

Các câu hỏi dưới đây có thể giống với câu hỏi trên

Thanh Tùng DZ

24 tháng 10 2016 - olm

tìm số tự nhiên n để :

a) 7n + 8 chia hết cho n

b) 35 - 12n chia hết cho n ( n < 3 )

c) n + 8 chia hết cho n + 3

giúp nha, giải đầy đủ

#Hỏi cộng đồng OLM #Toán lớp 6

Lê Nguyên Hạo

24 tháng 10 2016

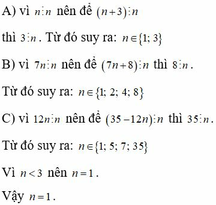
a) $\frac{7n+8}{n}=\frac{7n}{n}+\frac{8}{n}=7+\frac{8}{n}$

$\Rightarrow n\in\text{Ư}\left(8\right)=\left\{1;2;4;8\right\}$

b) $\frac{35-12n}{n}=\frac{35}{n}-\frac{12n}{n}=\frac{35}{n}-12$

$\Rightarrow n\in\text{Ư}\left(35\right)=\left\{1;3;5;7;35\right\}$

Loại $n\in\left\{1;3\right\}$ vì n > 3.

Vậy: $n\in\left\{5;7;35\right\}$

c) $\frac{n+8}{n+3}=\frac{n+3+5}{n+3}=\frac{n+3}{n+3}+\frac{5}{n+3}=1+\frac{5}{n+3}$

$\Rightarrow n+3\in\text{Ư}\left(5\right)=\left\{1;5\right\}$

$\Rightarrow n+3=1\Rightarrow n=1-3=-2$ (loại vì -2 < 0)

$\Rightarrow n+3=5\Rightarrow n=2$

Vậy: n = 2

Đúng(0)

ngonhuminh

24 tháng 10 2016

giải đầy đủ ba câu nhưng không yêu cầu chi tiết

a. n phải chia hết cho n rồi cãi sao đuọc

7 n càng chia hết cho n

vậy 8 phải chia hết cho n

n=(1.2.4.8)

b. ồ n<3 thì còn mỗi 1.2 n=1 hiển nhiên rồi, n=2 ko cần tử biết loại

vậy n=1 (người ra câu nàylãng xẹt)

c. (n+8)/(n+3) ko có dấu chia hết tạm dùng (...) là dấu chia hết

(n+3) (...) (n+3) hiển nhiên

(n+8) (...) (n+3)

=>[n+8-(n+3)] (...)(n+3)

5(...)(n+3)

vậy n+3=(1,5)

n=(2)

Đúng(0)

ngophamquynh tram

9 tháng 12 2018 - olm

tìm các số tự nhiên a và b sao cho a.b=105 và a<b

chứng tỏ rằng với mọi số tự nhiên n thì (n+2017).(n+2018) luôn chia hết cho 2

chứng tỏ rằng với mọi số tự nhiên n thì (n+8).(n+12). (n+7)luôn chia hết cho 3

giúp mình với mình đang gấp!

#Hỏi cộng đồng OLM #Toán lớp 6

Yến Nhi

13 tháng 7 2016

Tìm số tự nhiên n,để:

a) n+4:n

b) 5n-6:n (n<1)

c) 143-12n:n (với n<12)

#Hỏi cộng đồng OLM #Toán lớp 6

Nguyễn Lê Phước Thịnh

30 tháng 1 2022

a: $\Leftrightarrow n\inƯ\left(4\right)$

hay $n\in\left\{1;2;4\right\}$

b: $\Leftrightarrow n\in\left\{1;2;3;6\right\}$

mà n<1

nên $n\in\varnothing$

c: $\Leftrightarrow n\inƯ\left(143\right)$

mà n<12

nên $n\in\left\{1;11\right\}$

Đúng(0)

Yến Nhi

11 tháng 7 2016

Tìm số tự nhiên n,để:

a) n+4:n

b) 5n-6:n (n<1)

c) 143-12n:n (với n<12)

#Hỏi cộng đồng OLM #Toán lớp 6

phuong phuong

11 tháng 7 2016

Đúng(0)

Yến Nhi

13 tháng 7 2016

Đúng(0)

Midori takamine

28 tháng 1 2016 - olm

1) Viết tập hợp các số nguyên x biết :

a) -35/7<x<-1

b)-18/6<x<144/72

c)-30/5<x<-45/9

d)-60/12<x<20/5

2)Cho phân số 19/44.Phải thêm vào phần tử và mẫu của phấn số với số tự nhiên nào để được phân số bằng phân số 22/47

3)Tìm n thuộc Z để các phân số sau là số nguyên : A=n/n-4 B=2n+7/n+3

#Hỏi cộng đồng OLM #Toán lớp 6

huỳnh thị ngọc ngân

28 tháng 1 2016

a) x = -4 ; -3 ; -2

b) x = -2 ; -1 ; 0 ; 1

c) không có x nào thỏa mãn trường hợp trên

d) x = -4 ; -3 ; -2 ; -1 ; 0 ; 1 ;2 ; 3

Đúng(0)

Pham Trong Bach

27 tháng 9 2018

Tìm số tự nhiên n để:a, (n+3) ⋮ nb, (7n+8) ⋮ nc, (35 - 12n) ⋮ n với n <...

Đọc tiếp

#Hỏi cộng đồng OLM #Toán lớp 6

Cao Minh Tâm

27 tháng 9 2018

a, Vì n ⋮ n nên để (n+3) ⋮ n thì 3 ⋮ n. Từ đó suy ra: n ∈ {1;3}

b, Vì 7n ⋮ n nên để (7n+8) ⋮ n thì 8 ⋮ n. Từ đó suy ra: n ∈ {1;2;4;8}

c, Vì 12n ⋮ n nên để (35 - 12n) ⋮ n thì 35 ⋮ n. Từ đó suy ra: n ∈ {1;5;7;35}

Vì n < 3 nên n = 1

Vậy n = 1

Đúng(0)

hưng việtnam

11 tháng 10 2024

(n+3):3

Đúng(0)

nhật

5 tháng 5 2016 - olm

Tìm số tự nhiên n nhỏ nhất để cho các phân số sau đều tối giản: 7/(n+10);8/(n+11);9/(n+12);...;35/n+38

Cảm ơn trước ạ

#Hỏi cộng đồng OLM #Toán lớp 6

Bùi Hồng Sang

26 tháng 4 2020 - olm

a) Chứng minh rằng với mọi số tự nhiên n thì phân số 21n+4/14n+3 là phân số tối giản

b) Tìm tất cả các số tự nhiên n để phân số n+3/n-12 là phân số tối giản

c) Tìm các số tự nhiên n để phân số 21n+3/6n+4 rút gọn được

#Hỏi cộng đồng OLM #Toán lớp 6

Diệu Anh

26 tháng 4 2020

a) Để 21n+4/14n+3 là phân số tổi giản thì ƯCLN(21n+4; 14n+3) =1

Gọi ƯCLN(21n+4; 14n+3) =d => 21n+4 $⋮$d; 14n+3 $⋮$d

=> (14n+3) -(21n+4) $⋮$d

=> 3(14n+3) -2(21n+4) $⋮$d

=> 42n+9 - 42n -8 $⋮$d

=> 1$⋮$d

=> 21n+4/14n+3 là phân số tối giản

Vậy...

c) Gọi ƯC(21n+3; 6n+4) =d; 21n+3/6n+4 =A => 21n+3 $⋮$d; 6n+4 $⋮$d

=> (6n+4) - (21n+3) $⋮$d

=> 7(6n+4) - 2(21n+3) $⋮$d

=> 42n +28 - 42n -6$⋮$d

=> 22 $⋮$cho số nguyên tố d

d $\in${11;2}

Nếu phân số A rút gọn được cho số nguyên tố d thì d=2 hoặc d=11

Nếu A có thể rút gọn cho 2 thì 6n+4 luôn luôn chia hết cho 2. 21n+3 chia hết cho 2 nếu n là số lẻ

Nếu A có thể rút gọn cho 11 thì 21n+3 $⋮$11 => 22n -n +3$⋮$11 => n-3 $⋮$11 Đảo lại với n=11k+3 thì 21n+3 và 6n+4 chia hết cho 11

Vậy với n là lẻ hoặc n là chẵn mà n=11k+3 thì phân số đó rút gọn được

Đúng(0)

Linh Nguyễn

26 tháng 8 2015 - olm

Bài 1: Cho n thuộc N. Tìm số tự nhiên N và nhỏ hơn N+1

Bài 2: Tìm các số tự nhien a, b, c đồng thời thỏa mãn 3 điều kiện: a<b<c ; 11<a<15 ; 12<c<15

#Hỏi cộng đồng OLM #Toán lớp 6

OoO Kún Chảnh OoO

26 tháng 8 2015

ta có a<b<c=>a<c (1)

ta có 11<a mà c<11 =>c<11<a=>c<a (2)

từ (1)&(2)=> a &c mâu thuẫn với nhau vậy a,b,c không tồn tại để thỏa mãn điều kiện trên

tick đúng cho mình đi mình đã làm dùm bạn mòa

Đúng(1)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP