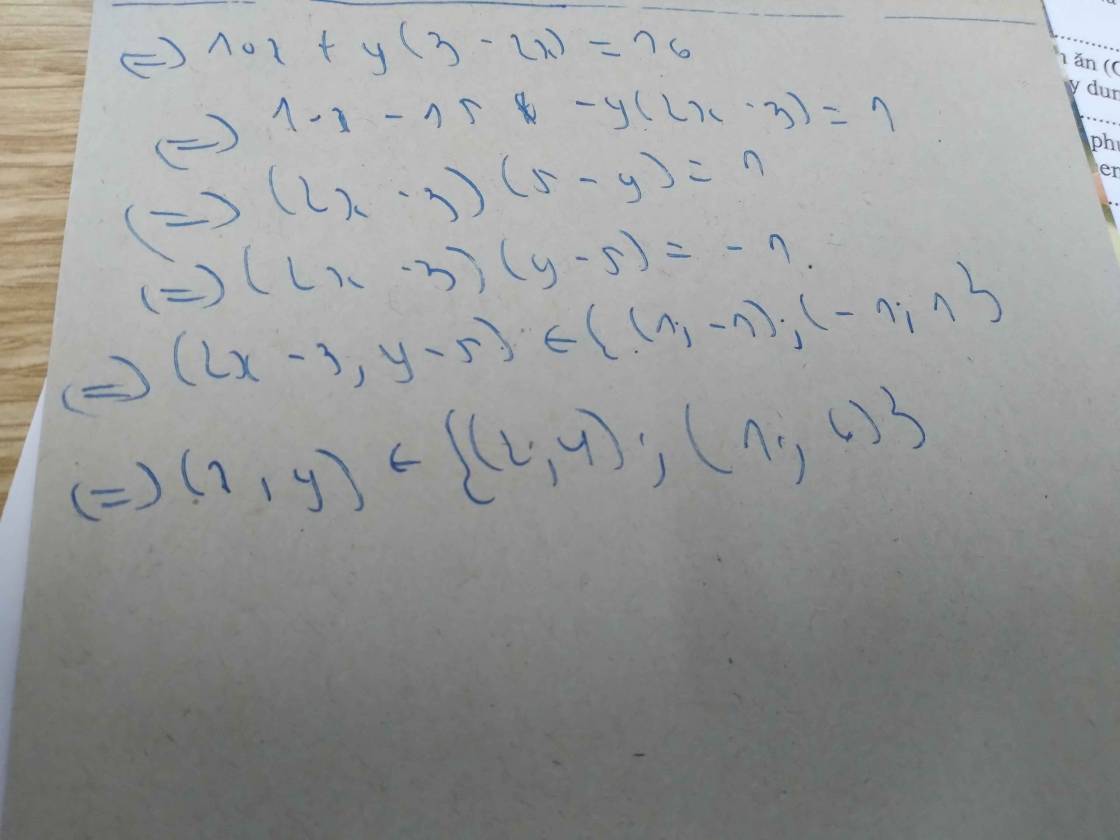GN
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HD
1
H
1
2 tháng 3 2023
=>3y(2x+1)-10x-5=7
=>(2x+1)(3y-5)=7
=>\(\left(2x+1;3y-5\right)\in\left\{\left(1;7\right);\left(7;1\right)\right\}\)(Vì x,y là số nguyên)
=>\(\left(x,y\right)\in\left\{\left(0;6\right);\left(3;2\right)\right\}\)
TK
1
13 tháng 3 2017
6xy-3y-4x=4
3y.(2x-1)-2.(2x-1)=6
(2x-1).(3y-2)=6
vì x,y là số nguyên nên ta có : x=-1,y=3
KN
1
RR
16 tháng 5 2018
pt <=> 3y(2x + 1) - 4x - 2 = -55
<=> 3y(2x + 1) - 2(2x + 1) = -55
<=> (3y - 2)(2x + 1) = -55 = (-1).55 = 55.(-1) = (-5).11 = 11.(-5)
= (-55).1 = 1.(-55) = (-11).5 = 5.(-11)
Thay (3y - 2) và (2x + 1) vào 8 trường hợp trên là tìm được x,y
tất nhiên phải xét xem x,y có là số nguyên hay không
VK
1
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 1 2024
\(6xy-10x+3y=12\)
\(\Leftrightarrow6xy+3y-10x-5=7\)
\(\Rightarrow3y\left(2x+1\right)-5\left(2x+1\right)=7\)
\(\Leftrightarrow\left(2x+1\right)\left(3y-5\right)=7\)
Ta có bảng:
| 2x+1 | -7 | -1 | 1 | 7 |
| 3y-5 | -1 | -7 | 7 | 1 |
| x | -4 | -1 | 0 | 3 |
| y | 4/3 (loại) | -2/3 (loại) | 4 | 2 |
Vậy \(\left(x;y\right)=\left(0;4\right);\left(3;2\right)\)
LH
1
23 tháng 12 2023
xy+x-3y=0
=> (xy+x)-3y-3=0-3
=>x(y+1)-(3y+3)=(-3)
=>x(y+1)-3(y+1)=(-3)
=>(y+1).(x-3)=(-3)
Mà (-3)=1.(-3)=(-1).3
Lập bảng giá trị:
| x-3 | 1 | -1 | 3 | -3 |
| y+1 | -3 | 3 | -1 | 1 |
| x | 4 | 2 | 6 | 0 |
| y | -4 | 2 | -2 | 0 |
Vậy các cặp số nguyên (x;y) là (4;-4);(2;2);(6;-2);(0;0)
DM
1
28 tháng 12 2020
Ta có: \(6xy-8x-3y-2=0\)
\(\Leftrightarrow6xy-3y-8x+4-6=0\)
\(\Leftrightarrow3y\left(2x-1\right)-4\left(2x-1\right)=6\)
\(\Leftrightarrow\left(2x-1\right)\left(3y-4\right)=6\)
\(\Leftrightarrow\left(2x-1\right);\left(3y-4\right)\inƯ\left(6\right)\)
\(\Leftrightarrow\left(2x-1\right)\left(3y-4\right)\in\left\{1;-1;2;-2;3;-3;6;-6\right\}\)
mà 2x-1 lẻ và \(2x-1\ge-1\) \(\forall x\in N\)
nên \(\left(2x-1\right)\in\left\{-1;1;-3;3\right\}\) và \(\left(3y-4\right)\in\left\{2;-2;6;-6\right\}\)
Trường hợp 1:
\(\left\{{}\begin{matrix}2x-1=-1\\3y-4=-6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x=0\\3y=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=-\dfrac{2}{3}\left(loại\right)\end{matrix}\right.\)
Trường hợp 2:
\(\left\{{}\begin{matrix}2x-1=1\\3y-4=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x=2\\3y=10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=\dfrac{10}{3}\left(loại\right)\end{matrix}\right.\)
Trường hợp 3:
\(\left\{{}\begin{matrix}2x-1=-3\\3y-4=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x=-2\\3y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-1\\y=\dfrac{2}{3}\left(loại\right)\end{matrix}\right.\)
Trường hợp 4:
\(\left\{{}\begin{matrix}2x-1=3\\3y-4=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x=4\\3y=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=2\left(nhận\right)\end{matrix}\right.\)
Vậy: (x,y)=(2;2)
V
1
