AW
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
15 tháng 1 2020
d. Câu hỏi của Black - Toán lớp 7 - Học toán với OnlineMath
NN
1
HP
1 tháng 3 2016
Ta có:x2-2y2=1
<=>x2-1=2y2
<=>(x-1)(x+1)=2y2=y.2y
TH1:(x-1)(x+1)=2y2
=>x-1=2 và x+1=y2
=>x=3 và x+1=y2=>y2=3+1=4=>y=2
TH2:(x-1)(x+1)=y.2y
=>x-1=y và x+1=2y
=>x=y+1 và x+1=2y=>(y+1)+1=2y=>y+2=2y=>2y-y=2=>y=2
do đó x=y+1=2+1=>x=3
vậy (x;y)=(3;2)
NT
1
HP
5 tháng 3 2016
x2-2y2=1
<=>x2-1=2y2
<=>(x-1)(x+1)=2y2=y.2y
+)(x-1)(x+1)=2y2
=>x-1=2 và x+1=y2
=>x=3 và x+1=y2
thay x=3 vào x+1=y2=>y2=3+1=4=>y=2(vì y nguyên tố nên ko thể là -2)
do đó (x;y)=(3;2)
+)(x-1)(x+1)=y.2y
=>x-1=y và x+1=2y
=>x=y+1 và x+1=2y
thay x=y+1 vào x+1=2y=>(y+1)+1=2y=>y+2=2y=>2y-y=2=>y=2
khi đó x=2+1=3
Do đó (x;y)=(3;2)
Vậy (x;y)=(3;2)
ML
2
17 tháng 9 2021
Ta có: x^2 – 2x + 1 = 6y^2 -2x + 2
=> x^2 – 1 = 6y^2 => 6y^2 = (x-1).(x+1) chia hết cho 2 , do 6y^2 chia hết cho 2
Mặt khác x-1 + x +1 = 2x chia hết cho 2 => (x-1) và (x+1) cùng chẵn hoặc cùng lẻ.
Vậy (x-1) và (x+1) cùng chẵn => (x-1) và (x+1) là hai số chẵn liên tiếp
(x-1).(x+1) chia hết cho 8 => 6y^2 chia hết cho 8 => 3y^2 chia hết cho 4 => y^2 chia hết cho 4 => y chia hết cho 2
y = 2 ( y là số nguyên tố) , tìm được x = 5
17 tháng 9 2021
Có cách dễ hơn mà :>>
Ta có :
6y2 + 1 = x2
Vì 6y2 chẵn và 1 lẻ => x2 là số chính phương lẻ
=> x2 chia 8 dư 1 => x - 1 ⋮ 8
Vì 6y2 + 1 = x2 => 6y2 = x2 - 1 ⋮ 8
=> 3y2 ⋮ 4 => y2 ⋮ 4 ( do ( 3 , 4 ) = 1 )
=> y ⋮ 2 mà y là số nguyên tố
=> y = 2 => x = 5
LM
1
5 tháng 3 2015
Ta có: x2-2y2=1
x2-1=2y2(x-1)(x+1)=2y2
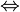x2-1=2y2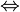(x-1)(x+1)=2y2vì 2y2\( {\vdots}\)2 nên (x-1)(x+1)\( {\vdots}\)2
vì x-1+x+1=2x 
x-1 và x+1 có cùng tính chẵn lẻ
(x-1)(x+1) là hai số chẵn liên tiếp
(x-1)(x+1)\( {\vdots}\)4 2y2\( {\vdots}\)4 y2\( {\vdots}\)2 y\( {\vdots}\)2 y = 2
Và từ y=2 ta thay vào x2-2y2=1 x2-2.22=1 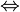x2 = 9 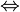x = 3
Vật số nguyên tố (x, y) là cặp số (3, 2)