
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
GN
2

Các câu hỏi dưới đây có thể giống với câu hỏi trên

CM
31 tháng 7 2019
Đáp án A
Ta có
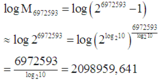
Do đó số chữ số của số đó là 2098959 + 1 = 2098960
PD
1

CM
24 tháng 6 2018
Đáp án B.
Ta có: Phần thực: –4, phần ảo: –3
![]()
Hai ý (3) và (4) sai.


Cho \(p=2,p=3\) ta thấy không thỏa mãn.
Cho \(p=5\) ta thấy thỏa mãn.
Xét \(p>5\), khi đó \(p⋮̸5\). Khi đó \(p^2\equiv1,4\left[5\right]\) (tính chất của scp)
Khi \(p^2\equiv1\left[5\right]\) thì \(p^2+1⋮5\), khi \(p^2\equiv4\left[5\right]\) thì \(p^2+6⋮5\) nên 1 trong 2 số này là hợp số, không thỏa mãn.
Vậy \(p=5\) là snt duy nhất thỏa mãn ycbt.
Đây là dạng toán nâng cao chuyên đề số nguyên tố, cấu trúc thi chuyên, thi học sinh giỏi các cấp. Hôm nay, Olm sẽ hướng dẫn các em giải chi tiết dạng này bằng phương pháp đánh giá như sau.
+ Nếu p = 2 ta có: p2 + 4 = 22 + 4 = 4 + 4 = 8 (loại)
+ Nếu p = 3 ta có: p2 + 6 = 32 + 6 = 9 + 6 = 15 (loại)
+ Nếu p = 5 ta có: p2 + 4 = 52 + 4 = 25 + 4 = 29 (thỏa mãn)
p2 + 6 = 52 + 6 = 25 + 6 = 31 (thỏa mãn)
+ Nếu p > 5 khi đó: p2 : 5 dư 1 hoặc 4 (tính chất số chính phương)
TH1 p2 : 5 dư 1 ⇒ p2 + 4 ⋮ 5 (là hợp số loại)
TH2 p2 : 5 dư 4 \(\Rightarrow\) p2 + 6 ⋮ 5 (là hợp số loại)
Từ những lập luận trên ta có:
p = 5 là giá trị số nguyên tố duy nhất thỏa mãn đề bài
Kết luận số nguyên tố thỏa mãn đề bài là 5.