Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Coi 2 số cần tìm là ab và cd (ab>cd)
ta có hiệu hai số là ab - cd =16
và abcd +cdab=5454
abx100+cd+cdx100+ab=5454
=>abx101+cdx101=5454
=>101x(ab+cd)=5454
=>ab+cd=5454:101
=>ab+cd=54
vậy tổng ab+cd=54
=>ab=(54 +16):2=35

Gọi số đó là ab
Theo bài ra ta có:
ab x 50=1ab0
=>ab x 50=1000+a00+b0
=>ab x 50=1000+100 x a+ b x 10
=>(10a+b) x 50=1000+100 x a+10 x b
=>500 x a+50 x b=1000+100 x a+10 x b
=>500a+50b-100a-10b=1000
=>(500a-100a)+(50b-10b)=1000
=>400a+40b=1000
=>40 x 10 x a+40 x b=1000
=>40 x (10a+b)=1000
=>10a+b=1000:40=25
=>ab=25
Vậy số cần tìm là 25
* 500a=500 x a
Tick mk nhé

7/ Em sửa lại đề ạ
Cho hai số thực dương a, b thỏa mãn a+b=4ab
Chứng minh rằng \(\frac{a}{4b^2+1}+\frac{b}{4a^2+1}\ge\frac{1}{2}\)
Đổi biến \(\left(a,b\right)\rightarrow\left(\frac{1}{x},\frac{1}{y}\right)\)
Từ giả thiết => x+y=4
Ta có: BĐT cần CM tương đương với:
\(\frac{\frac{1}{x}}{\frac{4}{y^2}+1}+\frac{\frac{1}{y}}{\frac{4}{x^2}+1}\ge\frac{1}{2}\)\(\Leftrightarrow\frac{y^2}{x\left(4+y^2\right)}+\frac{x^2}{y\left(4+x^2\right)}\ge\frac{1}{2}\left(1\right)\)
Áp dụng BĐT Schwarz, ta có:
∑\(\frac{x^2}{y\left(4+x^2\right)}\ge\frac{\left(x+y\right)^2}{4\left(x+y\right)+xy^2+x^2y}=\frac{16}{16+xy^2+x^2y}\)
Ta chỉ cần chứng minh:
\(xy^2+x^2y\le16\Leftrightarrow xy^2+x^2y\le\frac{1}{4}\left(x+y\right)^3\)
\(\Leftrightarrow xy^2+x^2y\le x^3+y^3\)(luôn đúng)
Do đó (1) đúng. BĐT được chứng minh. Dấu "=" xảy ra khi x=y=2⇔a=b=\(\frac{1}{2}\)
6. (chuyên Hòa Bình)
Cho các số dương x, y, z thỏa mãn: xy+zx+4yz=32
Tìm giá trị nhỏ nhất của\(P=x^2+16y^2+16z^2\)
Áp dụng bất đẳng thức Cauchy cho ba số dương x,y,z ta có
\(\hept{\begin{cases}8y^2+\frac{1}{2}x^2\ge2\sqrt{8y^2.\frac{1}{2}x^2}=4xy\\8z^2+\frac{1}{2}x^2\ge2\sqrt{8z^2.\frac{1}{2}x^2}=4xz\\8y^2+8z^2\ge2\sqrt{8y^2.8z^2}=16yz\end{cases}}\)
Cộng từng vế của ba bđt trên ta có
\(P\ge4\left(xy+xz+4yz\right)=4.32=128\)

c1 chắc có lộn đề r
c2:Gọi 2 số cần tìm lần lượt là a,b
Ta có: 9/11a=6/7b
a+b=258 nên a=258-b
=>9/11*(258-b)=6/7b
2322/11-9/11b=6/7b
6/7b+9/11b=2322/11
66/77+63/77b=2322/11
129/77b=2322/11
b=2322/11:129/77=126
nên a=258-126=132
Vậy 2 số cần tìm lần lượt là 132;126

a: Gọi mẫu là x
Theo đề, ta có:
\(\dfrac{2}{5}< \dfrac{4}{x}< \dfrac{2}{3}\)
=>10>x>6
=>\(x\in\left\{9;8;7\right\}\)
b: Phần phân số là 1-9/25=16/25
Phần nguyên là 125x9/25=45
Vậy: Hỗn số cần tìm là \(45\dfrac{16}{25}\)

gọi số đó là abc(a,b,c là các số khác nhau)
=>abc=ab+bc+ca+ba+cb+ac
=>abc=a0+b+b0+c+c0+a+b0+a+c0+b+a0+c
=>abc=2aa+2bb+2cc
=>78a=12b+21c<12.9+21.9=297
=>a<4=>a=1;2;3
vì abc lớn nhất nên ta chọn a=3=>12b+21c=234
=>4b+7c=78
chọn b lớn nhất có thể : thử b=9=>c=6(nhận)
vậy số lớn nhất đó là 396

Chọn đáp án B.
Bằng cách sử dụng điều kiện tồn tại nghiệm của phương trình, chúng ta có: Khi a = 0 thì hàm số chỉ đạt giá trị lớn nhất (khi b < 0) hoặc chỉ đạt giá trị nhỏ nhất (khi b > 0). Còn khi
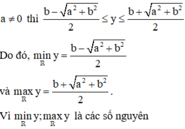
nên tập giá trị của hàm số đã cho chỉ có đúng 6 số nguyên khi và chỉ khi
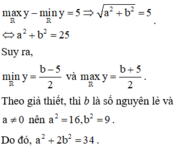

Theo bài ra: $8\frac{a}{b}=\frac{a}{b-a}\leftrightarrow a(8a-7b)=0\leftrightarrow a=0$ hoặc $8a=7b$.Suy ra công thức tối giản của phân số đó là $0$ hoặc $\frac{7}{8}$.
\(\frac{a}{b-a}=8.\frac{a}{b}\)
\(=>ab=8a.\left(b-a\right)=8ab-8a^2\)
\(=>8a^2=8ab-ab=7ab\)
\(=>8a=7b=>\frac{a}{b}=\frac{7}{8}\) (thỏa mãn a/b tối giản)
Lời giải:
Gọi số cần tìm là $\overline{abcdef}$ với $a,b,c,d,e,f$ là số tự nhiên có 1 chữ số, $a\geq 1$ và $a+b+c+d+e+f=42$
Để số nhỏ nhất thì $a$ nhỏ nhất có thể
$\Rightarrow a=1$
$\Rightarrow b+c+d+e+f=41$
Do $c,d,e,f\leq 9$ nên $b=41-c-d-e-f\geq 41-9-9-9-9=5$
Để $\overline{abcdef}=\overline{1bcdef}$ nhỏ nhất thì $b$ nhỏ nhất
$\Rightarrow b=5$
Khi đó: $c+d+e+f=41-5=36$. Do $c,d,e,f$ là số tự nhiên có 1 chữ số nên $c=d=e=f=9$
Vậy số nhỏ nhất cần tìm là $159999$