V
3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
VN
20 tháng 12 2016
Quy luật là: Số đằng sau hơn số đằng trước 1111 đơn vị
Ví dụ: 1234 + 1111 = 2354
2354 + 1111 = 3465
3465 + 1111 = 4576
Số số hạng dãy trên có là:
( 6798 - 1243 ) : 1111 + 1 = 6 (số)
Tổng của dãy trên là:
( 6798 + 1243 ) x 6 : 2 = 24123
10 tháng 5 2017
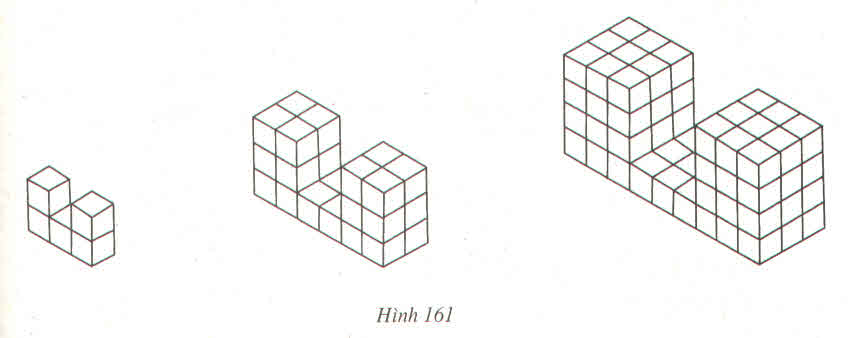
Số hình lập phương ở hình 1: 1.3+1.1.2=5 (khối)
Số hình lập phương ở hình 2:22.3+22.2.2=28 (khối)
Số hình lập phương ở hình 3:32.3+32.3.2=81 (khối)
\(\Rightarrow\)Công tức tính:
Số hình lập phương ở hình x: x2.3+x2.x.2 (khối)
Số hình lập phương ở hình 10 là:102.3+102.10.2=2300 (khối)
5 tháng 7 2017
Cách 1 : Khi ta vẽ hình thứ tư thì :
Số hình lập phương đơn vị ở phía trái là 4.5.4=80
29 tháng 5 2018
a) Sorry mình mới lớp 7 :)
b)
12 km phải trả số tiền là : 12000 + 10000 . 11 = 122000
Vậy.........
29 tháng 5 2018
ấy mà đề nó cứ sai sai ấy đáng ra 1 km đầu là 10000 sau đó là 12000 chứ :)
a,
Gọi x là số km người đó đi
Hàm biểu diễn tiền xe:
12000+(x-1)*10000 (vnđ)
b,
Thay x=12 khi đó:
12000+(12-1)*10000=122000 (vnđ)
Chúc bạn học tốt!
PN
19 tháng 9 2017
Lương Tịch bn tham khảo nha
I > Phương pháp dự đoán và quy nạp :
Trong một số trường hợp khi gặp bài toán tính tổng hữu hạn
Sn = a1 + a2 + .... an (1)
Bằng cách nào đó ta biết được kết quả (dự đoán , hoặc bài toán chứng minh khi đã cho biết kết quả). Thì ta nên sử dụng phương pháp này và hầu như thế nào cũng chứng minh được .
Ví dụ 1 : Tính tổng Sn =1+3+5 +... + (2n -1 )
Thử trực tiếp ta thấy : S1 = 1
S2 = 1 + 3 =22
S3 = 1+ 3+ 5 = 9 = 32
... ... ...
Ta dự đoán Sn = n2
Với n = 1;2;3 ta thấy kết quả đúng
giả sử với n= k ( k 1) ta có Sk = k 2 (2)
ta cần phải chứng minh Sk + 1 = ( k +1 ) 2 ( 3)
Thật vậy cộng 2 vế của ( 2) với 2k +1 ta có
1+3+5 +... + (2k – 1) + ( 2k +1) = k2 + (2k +1)
vì k2 + ( 2k +1) = ( k +1) 2 nên ta có (3) tức là Sk+1 = ( k +1) 2
theo nguyên lý quy nạp bài toán được chứng minh
vậy Sn = 1+3=5 + ... + ( 2n -1) = n2
Tương tự ta có thể chứng minh các kết quả sau đây bằng phương pháp quy nạp toán học .
1, 1 + 2+3 + .... + n =
2, 12 + 2 2 + ..... + n 2 =
3, 13+23 + ..... + n3 =
4, 15 + 25 + .... + n5 = .n2 (n + 1) 2 ( 2n2 + 2n – 1 )
8*2+4=20 ; 20*2+4=44, 44*2+4 = 92. Vậy số tiếp theo là 92*2+4 =188.
Theo quy luật: xn=2xn-1+4
=> Số tiếp theo là: 92*2+4=188