Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Tập hợp các điểm biểu diễn các số phức z là các hình sau:
a) Ta có x = 1, y tùy ý nên tập hợp các điểm biểu diễn z là đường thẳng x = 1 (hình a)
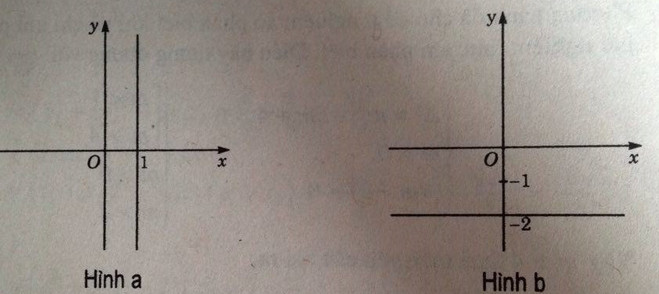
b) Ta có y = -2, x tùy ý nên tập hợp các điểm biểu diễn z là đường thẳng y = -2 (hình b)
c) Ta có x ∈ [-1, 2] và y ∈ [0, 1] nên tập hợp các điểm biểu diễn z là hình chữ nhật sọc (hình c)
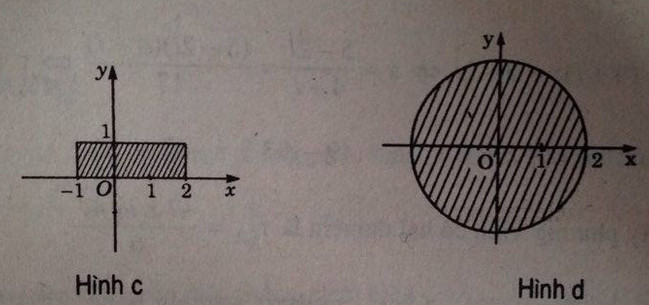
d) Ta có:
|z|≤2⇔√x2+y2≤2⇔x2+y2≤4|z|≤2⇔x2+y2≤2⇔x2+y2≤4
Vậy tập hợp các điểm biểu diễn z là hình tròn tâm O (gốc tọa độ) bán kính bằng 2 (kể cả các điểm trên đường tròn) (hình d)

Lời giải:
Thiết diện là một tam giác đều cạnh \(a\sqrt{3}\) nên \(2R=\sqrt{3}a\Rightarrow R=\frac{\sqrt{3}a}{2}\)
Do đó diện tích xq của hình nón là:
\(S_{xq}=\pi Rl=\frac{3a^2}{2}\pi\)
Đáp án C

Giả sử z = a + bi
Khi đó: |z|=√a2+b2|z|=a2+b2
Từ đó suy ra:
|z|=√a2=|a|≥a,|z|=√b2=|b|≥b

Lời giải:
Đặt \(z=a+bi\) với $a,b$ là các số thực.
Ta có: \(|z+2-i|=|(a+2)+i(b-1)|=2\sqrt{2}\)
\(\Leftrightarrow (a+2)^2+(b-1)^2=8(*)\)
Và:
\((z-1)^2=z^2+1-2z=(a+bi)^2+1-2(a+bi)\)
\(=a^2-b^2+2abi+1-2(a+bi)\)
\(=(a^2-b^2+1-2a)+i(2ab-2b)\)
Để \((z-1)^2\) thuần ảo thì \(a^2-b^2+1-2a=0\)
\(\Leftrightarrow (a-1)^2=b^2\)
\(\Leftrightarrow \left[\begin{matrix} a-1=b\\ a-1=-b\end{matrix}\right.\Leftrightarrow \left[\begin{matrix} a=b+1\\ a=1-b\end{matrix}\right.\)
Nếu \(a=b+1\), thay vào (*):
\((b+3)^2+(b-1)^2=8\Leftrightarrow b^2+2b+1=0\Leftrightarrow b=-1\)
\(\Rightarrow a=0\Rightarrow z=-1\)
Nếu \(a=1-b\Rightarrow (3-b)^2+(b-1)^2=8\)
\(\Leftrightarrow b^2-4b+1=0\Rightarrow b=2\pm \sqrt{3}\)
\(\Rightarrow a=-1\mp \sqrt{3}\), tương ứng với 2 số $z$
Vậy có $3$ số thỏa mãn.

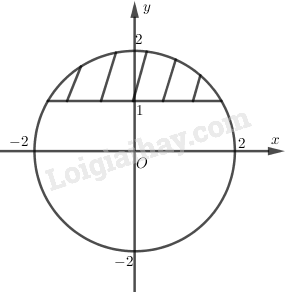
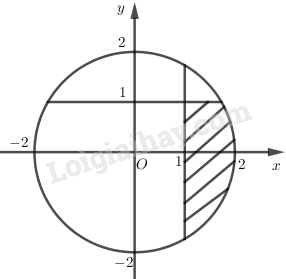
Chọn B.
Ta có: