
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a)11x-7<8x+7
<-->11x-8x<7+7
<-->3x<14
<--->x<14/3 mà x nguyên dương
---->x \(\in\){0;1;2;3;4}
b)x^2+2x+8/2-x^2-x+1>x^2-x+1/3-x+1/4
<-->6x^2+12x+48-2x^2+2x-2>4x^2-4x+4-3x-3(bo mau)
<--->6x^2+12x-2x^2+2x-4x^2+4x+3x>4-3+2-48
<--->21x>-45
--->x>-45/21=-15/7 mà x nguyên âm
----->x \(\in\){-1;-2}

1.
\(A=\frac{2x^3+x^2+2x+4}{2x+1}=\frac{x^2(2x+1)+(2x+1)+3}{2x+1}=x^2+1+\frac{3}{2x+1}\)
Với $x$ nguyên, để $A$ nguyên thì $3\vdots 2x+1$
$\Rightarrow 2x+1\in \left\{1; -1; 3; -3\right\}$
$\Rightarrow x\in \left\{0; -1; 1; -2\right\}$
2.
\(B=\frac{3x^2-8x+1}{x-3}=\frac{3x(x-3)+x+1}{x-3}=\frac{3x(x-3)+(x-3)+4}{x-3}=3x+1+\frac{4}{x-3}\)
Với $x$ nguyên, để $B$ nguyên thì $4\vdots x-3$
$\Rightarrow x-3\in \left\{\pm 1; \pm 2; \pm 4\right\}$
$\Rightarrow x\in \left\{2; 4; 5; 1; 7; -1\right\}$

MK ko biế đúng ko nữa , sai thì ý kiến
a)
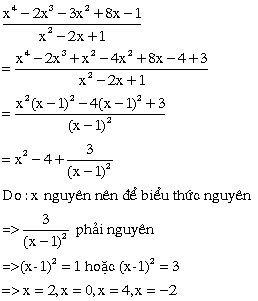
b)
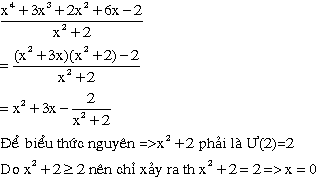
Chúc các bn hok tốt
Tham khảo nhé


bài 2 :
x3+7y=y3+7x
x3-y3-7x+7x=0
(x-y)(x2+xy+y2)-7(x-y)=0
(x-y)(x2+xy+y2-7)=0
\(\left\{{}\begin{matrix}x-y=0\Rightarrow x=y\left(loại\right)\\x^{2^{ }}+xy+y^2-7=0\end{matrix}\right.\)
x2+xy+y2=7 (*)
Giải pt (*) ta đc hai nghiệm phan biệt:\(\left[{}\begin{matrix}x=1va,y=2\\x=2va,y=1\end{matrix}\right.\)
\(y\left(x^2+1\right)=x^3-8x^2+2x\)
\(y=\frac{x^3-8x^2+2x}{x^2+1}\)
Vì y nguyên nên \(\left(x^3-8x^2+2x\right)⋮\left(x^2+1\right)\)
\(\left(x^3+x-8x^2-8+x+8\right)⋮\left(x^2+1\right)\)
\(\left[x\left(x^2+1\right)-8\left(x^2+1\right)+x+8\right]⋮\left(x^2+1\right)\)
\(\left(x^2+1\right)\left(x-8\right)+x+8⋮\left(x^2+1\right)\)
Vì \(\left(x^2+1\right)\left(x-8\right)⋮\left(x^2+1\right)\)
\(\Rightarrow\left(x+8\right)⋮\left(x^2+1\right)\)
\(\left(x+8\right)\left(x-8\right)⋮\left(x^2+1\right)\)
\(\left(x^2-64\right)⋮\left(x^2+1\right)\)
\(\left(x^2+1-65\right)⋮\left(x^2+1\right)\)
Vì \(\left(x^2+1\right)⋮\left(x^2+1\right)\)
\(\Rightarrow-65⋮\left(x^2+1\right)\)
\(\Rightarrow\left(x^2+1\right)\inƯ\left(65\right)=\left\{\pm1;\pm5;\pm13;\pm65\right\}\)
Mặt khác ta có : \(x^2+1>0\forall x\)nên :
\(\left(x^2+1\right)\in\left\{1;5;13;65\right\}\)
Vậy \(x\in\left\{0;\pm4;\pm8\right\}\)
Tiếp tục có bảng :
Vậy (x;y)={(0;0).(-8;-16)}
x bình phương công một bằng năm sao x tương ưng bằng công trừ bốn ? (Xem bảng hai) !