Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1 :
\(A=x^2-2xy^2+y^4=\left(x-y^2\right)^2=-\left(y^2-x\right)^2\)
Mà \(B=-\left(y^2-x\right)^2\)
Nên ta có : đpcm
Bài 2
Đặt \(\left(x+1\right)\left(x-2\right)\left(2x-1\right)=0\)
TH1 : x = -1
TH2 : x = 2
TH3 : x = 1/2
Bài 4 :
a, \(\left(2x+3\right)\left(5-x\right)=0\Leftrightarrow x=-\frac{3}{2};5\)
b, \(\left(x-\frac{1}{2}\right)\left(3x+1\right)\left(2-x\right)=0\Leftrightarrow x=\frac{1}{2};-\frac{1}{3};2\)
c, \(x^2+2x=0\Leftrightarrow x\left(x+2\right)=0\Leftrightarrow x=0;-2\)
d, \(x^2-x=0\Leftrightarrow x\left(x-1\right)=0\Leftrightarrow x=0;1\)

a) x3-x2+x-1=0
=>(x3-x2)+(x-1)=0
=>x2(x-1)+(x-1)=0
(x-1)(x2+1)=0
Ta có \(x^2+1>0\) ( vì \(x^2\ge0\) )
=>x-1=0
x=1
Vậy x=1 là nghiệm của f(x)
b)11x3+5x2+4x+10=0
=>(10x3+10)+(x3+x2)+(4x2+4x)=0
=>10(x3+1)+x2(x+1)+4x(x+1)=0
10(x+1)(x2-x+1)+x2(x+1)+4x(x+1)=0
(x+1)[10(x2-x+1)+x2+4x]=0
(x+1)(11x2-6x+10)=0
(x+1)[(9x2-2.3x+1)+9]=0
(x+1)[(3x-1)2+2x2+9]=0
=>x+1=0
x=-1
Vậy -1 là nghiệm của y(x)
c)-17x3+8x2-3x+12=0

dsahsfgfthsgdgfbbbbshsgfhdgjmafhtgyaemtjfbheyhfmyngehmrjbfgywagejmfhrbhhjgf
Trả lời:
\(g\left(x\right)=2x^3-11x^2-23x+14=0\)
\(\Leftrightarrow2x^3-14x^2+3x^2-21x-2x+14=0\)
\(\Leftrightarrow2x^2.\left(x-7\right)+3x.\left(x-7\right)-2.\left(x-7\right)=0\)
\(\Leftrightarrow\left(x-7\right).\left(2x^2+3x-2\right)=0\)
\(\Leftrightarrow\left(x-7\right).\left(2x^2-x+4x-2\right)=0\)
\(\Leftrightarrow\left(x-7\right).\left[x.\left(2x-1\right)+2.\left(2x-1\right)\right]=0\)
\(\Leftrightarrow\left(x-7\right).\left(2x-1\right).\left(x+2\right)=0\)
\(\Leftrightarrow\hept{\begin{cases}x-7=0\\2x-1=0\\x+2=0\end{cases}\Leftrightarrow}\hept{\begin{cases}x=7\\x=\frac{1}{2}\\x=-2\end{cases}}\)
Vậy đa thức có 3 nghiêm \(x=\left\{7,\frac{1}{2},-2\right\}\)

\(f_{\left(x\right)}-g_{\left(x\right)}=2x^5+x^4+1x^2+x+1-\left(2x^5+x^4-x^2+1\right)\)
\(=2x^5+x^4+1x^2+x+1-2x^5-x^4+x^2-1\)
\(=\left(2x^5-2x^5\right)+\left(x^4-x^4\right)+\left(1x^2+x^2\right)+x+\left(1-1\right)\)
\(=2x^2+x\)
+, Đặt \(2x^2+x=0\)
\(\Leftrightarrow x.2x=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=0\\2x=0\end{cases}}\Leftrightarrow x=0\)

\(x=-2\) là một nghiệm của \(P\left(x\right)\)nên
\(P\left(-2\right)=0\)
\(\Leftrightarrow\left(a+1\right)^2.\left(-2\right)^3+\left(2a-3\right).2^2-5=0\)
\(\Leftrightarrow-8\left(a^2+2a+1\right)+4\left(2a-3\right)-5=0\)
\(\Leftrightarrow-8a^2-8a-25=0\)
\(\Leftrightarrow-8\left(a^2+a+\frac{1}{4}\right)-23=-8\left(a+\frac{1}{2}\right)^2-23=0\)
Phương trình này vô nghiệm do \(VT< 0\).
Vậy không tồn tại giá trị nào của \(a\)thỏa mãn ycbt.

Bài 1:
a) \(x^2+7x-8=x^2+2.x.\frac{7}{2}+\frac{49}{4}-\frac{81}{4}\)
\(=\left(x+\frac{7}{2}\right)^2-\frac{81}{4}=0\)
\(\Rightarrow\left(x+\frac{7}{2}\right)^2=\frac{81}{4}\)
\(\Rightarrow\orbr{\begin{cases}x+\frac{7}{2}=\frac{9}{2}\\x+\frac{7}{2}=\frac{-9}{2}\end{cases}}\Rightarrow\orbr{\begin{cases}x=1\\x=-8\end{cases}}\)
Vậy nghiệm của đa thức m(x) là 1 hoặc -8
b) \(\left(x-3\right)\left(16-4x\right)=0\)
\(\Rightarrow\orbr{\begin{cases}x-3=0\\16-4x=0\end{cases}}\Rightarrow\orbr{\begin{cases}x=3\\x=4\end{cases}}\)
Vậy nghiệm của đa thức g(x) là 3 hoặc 4
c) \(5x^2+9x+4=0\)
\(\Rightarrow x^2+\frac{9}{5}x+\frac{4}{5}=0\)
\(\Rightarrow x^2+2x.\frac{9}{10}+\frac{81}{100}-\frac{1}{100}=0\)
\(\Rightarrow\left(x+\frac{9}{10}\right)^2-\frac{1}{100}=0\)
\(\Rightarrow\left(x+\frac{9}{10}\right)^2=\frac{1}{100}\)
\(\Rightarrow\orbr{\begin{cases}x+\frac{9}{10}=\frac{1}{10}\\x+\frac{9}{10}=\frac{-1}{10}\end{cases}}\Rightarrow\orbr{\begin{cases}x=\frac{-4}{5}\\x=-1\end{cases}}\)
Vậy...

\(P=x\left(5-2x\right)\)
\(x=0,,,,,,x=\frac{-5}{-2}\)
b/ \(\left(x^2-\frac{2.7x}{2}+\frac{49}{4}\right)+10-\frac{49}{4}=\left(x-\frac{7}{2}\right)^2-\frac{9}{4}=\left(x-\frac{7}{2}+\frac{3}{2}\right)\left(x-\frac{7}{2}-\frac{3}{2}\right)\)
\(x=2..........x=5\)
p/s tích phát
a,Ta ó: \(5x-2x^2=0\Leftrightarrow x\left(5-2x\right)=0\Leftrightarrow\orbr{\begin{cases}x=0\\5-2x=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=0\\x=\frac{5}{2}\end{cases}}}\)
Vậy...
b,Ta ó: \(Q\left(x\right)=x^2-7x+10=x^2-2x-5x+10=x\left(x-2\right)-5\left(x-2\right)=\left(x-5\right)\left(x-2\right)\)
\(Q\left(x\right)=0\Leftrightarrow\left(x-1\right)\left(x+5\right)=0\Leftrightarrow\orbr{\begin{cases}x-1=0\\x+5=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=1\\x=-5\end{cases}}}\)
Vậy...

a) Ta có: P(x) = 0 khi 3 – 2x = 0
=>-2x = -3 => x = \(\dfrac{3}{2}\)
b) Q(x) =x2 +2 là đa thức không có nghiệm vì
x2 ≥ 0
2 > 0 (theo quy tắc nhân hai số hữu tỉ cùng dấu)
=>x2 + 2 > 0 với mọi x
Nên Q(x) không có nghiệm trong R
a) Ta có P(x) = 0 khi 3 – 2x = 0
b) Đa thức Q(x) không có nghiệm, bởi vì:
x2 ≥ 0 với mọi x thuộc R.
2 > 0
\(\Rightarrow\) Q(x) = x2 + 2 > 0 với mọi x thuộc R.
Do đó, không có giá trị x nào thuộc R để Q(x) = 0 hay đa thức Q(x) không có nghiệm.
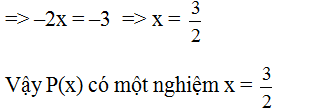
\(A\left(x\right)=2x^2-11x+5\)
\(A\left(x\right)=2x^2-x-10x+5\)
\(A\left(x\right)=x\left(2x-1\right)-5\left(2x-1\right)\)
\(A\left(x\right)=\left(2x-1\right)\left(x-5\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-1=0\\x-5=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}\\x=5\end{matrix}\right.\)
Ngọc Linh tìm nghiệm nha k phải tìm min