Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Vì 132 là số chẵn =>132 là tổng của 3 số nguyên tố =>1 trong 3 số phải la số chẵn => số chẵn đó bằng 2 mà là số ntố nhỏ nhất nên số nhỏ nhất đó là 2.
c)xét trường hợp p=2=> p+10=12 là hợp số loại
Xét trường hợp p= 3=> p+10= 13;p+20=23 đều là hợp số.
Xét trường hợp p>3 => p có 1 trong 2 dạng 3k+1;3k-1
với p= 3k +1=> p+20= 3k+21 chia hết cho 3
với p=3k-1=> p+10= 3k+9 chia hết cho 3
vậy p=3 thì p+10;p+20 đều là số ntố.

Câu 1:
Để B là số nguyên
=>5 chia hết cho n-3 hay n-3 thuộc vào Ư(5)={1;5;-1;-5}
Ta có bảng:
| n-3 | 1 | 5 | -1 | -5 |
| n | 4 | 8 | 2 | -2 |
| B | 5 | 1 | -5 | -1 |
=> n thuộc vào {4;8;2;-2} (thỏa mãn điều kiện n thuộc Z)

Ta có: \(n^3-n^2+n-1\)
\(=n^2\left(n-1\right)+\left(n-1\right)\)
\(=\left(n-1\right)\left(n^2+1\right)\)
Ta thấy \(n-1< n^2+1\) nên điều kiện cần để số trên là nguyên tố là: \(n-1=1\Rightarrow n=2\)
\(\Rightarrow n^3-n^2+n-1=5\) thỏa mãn
G/S ngược lại \(n-1\ne1\) thì \(n^2+1\ne1\)
\(\Rightarrow\left(n-1\right)\left(n^2+1\right)\) không là số nguyên tố (vô lý)
Vậy n = 2
Với n = 2
=> n3 - n2 + n - 1 = 5 (tm)
Với n > 2
=> \(\orbr{\begin{cases}n=2k+1\\n=2k\end{cases}}\left(k\inℕ^∗\right)\)
Với n = 2k + 1 khi đó : n3 - n2 + n - 1
= (n3 - n2) + (n - 1)
= n2(n - 1) + (n - 1)
= (n - 1)(n2 + 1)
= (2k + 1 - 1)[(2k + 1)2 + 1]
= 2k[(2k + 1)2 + 1] \(⋮\)2 (loại)
Với n = 2k
=> n3 - n2 + n - 1
= (n - 1)(n2 + 1)
= (2k - 1)[(2k)2 + 1]
= (2k - 1)(4k + 1) \(⋮2k-1\)(loại)
=> n = 2 là giá trị cần tìm

a)Ta có: n2+18n=n.(n+18)
Ư(n2+18n)={1,n,n+18,n.(n+18)}
Để n2+18n là số nguyên tố
=>Ư(n2+18n)={1,n.(n+18)}
=>n=1 hoặc n+18=1
Vì n+18>n
=>n=1
Vậy n=1

Đặt \(ƯC\left(3n^2+3n+4;n^2+n+1\right)=d\)
\(\Rightarrow3n^2+3n+4⋮d,n^2+n+1⋮d\)
\(\Rightarrow3n^2+3n+4-3\left(n^2+n+1\right)⋮d\)
\(\Rightarrow3n^2+3n+4-3n^2-3n-3⋮d\)
\(\Rightarrow1⋮d\Rightarrow d=1\)
Vậy với \(n\inℕ\) thì \(3n^2+3n+4\) và \(n^2+n+1\) nguyên tố cùng nhau.
1.Ta có
n4 + 4 = n4 + 4n2 + 4 – 4n2
= (n2 + 2 )2 – (2n)2
= (n2 + 2 – 2n )(n2 + 2 + 2n)
Vì n4 + 4 là số nguyên tố nên n2 + 2 – 2n = 1 hoặc n2 + 2 + 2n = 1
Mà n2 + 2 + 2n > 1 vậy n2 + 2 – 2n = 1 suy ra n = 1
Thử lại : n = 1 thì 14 + 4 = 5 là số nguyên tố
Vậy với n = 1 thì n4 + 4 là số nguyên tố./
2.Ta có :
n2003 + n2002 + 1 = n2(n2001 – 1) + n(n2001 – 1) + n2 + n + 1
Với n > 1 ta có :
Do đó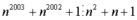
Mà n2 + n + 1 > 1 nên n2003 + n2002 + 1 là hợp số
Với n = 1 ta có
n2003 + n2002 + 1 = 12003 + 12002 + 1 = 3 là số nguyên tố .