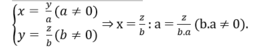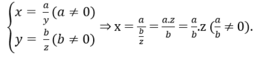Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: xy=k
nên y=x/k
yz=1
nên \(\dfrac{x}{k}\cdot z=1\)
=>xz=k
Vậy: x tỉ lệ nghịch với z theo hệ số tỉ lệ k
b: xy=k
y=z
nên x/k=z
=>x=kz
Vậy: x tỉ lệ thuận với z theo hệ số tỉ lệ k
c: x=ky
nên y=x/k
yz=1
nên \(\dfrac{xz}{k}=1\)
=>xz=k
Vậy: x tỉ lệ nghịch với z theo hệ số tỉ lệ k

a: x=2y
nên y=2/x
yz=-3
\(\Leftrightarrow z\cdot\dfrac{2}{x}=-3\)
\(\Leftrightarrow2z=-3x\)

a) Giả sử y tỉ lệ thuận với x theo hệ số tỉ lệ a nên \(y=a.x\) nên \(x=\dfrac{y}{a}\)
y tỉ lệ thuận với z theo hệ số tỉ lệ b nên \(y=b.z\)
Do đó, \(x=\dfrac{y}{a}=\dfrac{b.z}{a}=\dfrac{b}{a}.z\left(\dfrac{b}{a}\text{là hằng số vì a,b là các hằng số}\right)\)
Vậy x tỉ lệ thuận với z và hệ số tỉ lệ là \(\dfrac{b}{a}\)
b) Giả sử y tỉ lệ thuận với x theo hệ số tỉ lệ a nên y = a.x nên \(x=\dfrac{y}{a}\)
y tỉ lệ nghịch với z theo hệ số tỉ lệ b nên \(y=\dfrac{b}{z}\)
Do đó: \(x=\dfrac{y}{a}=\dfrac{\dfrac{b}{z}}{a}=\dfrac{b}{z}:a=\dfrac{b}{z}.\dfrac{1}{a}=\dfrac{\dfrac{b}{a}}{z}\left(\dfrac{b}{a}\text{là hằng số vì a,b là các hằng số}\right)\)
Vậy x tỉ lệ nghịch với z và hệ số tỉ lệ là \(\dfrac{b}{a}\)
c) Giả sử y tỉ lệ nghịch với x theo hệ số tỉ lệ a nên \(y=\dfrac{a}{x}\) nên \(x=\dfrac{a}{y}\)
y tỉ lệ nghịch với z theo hệ số tỉ lệ b nên \(y=\dfrac{b}{z}\)
Do đó: \(x=\dfrac{a}{y}=\dfrac{a}{\dfrac{b}{z}}=a:\dfrac{b}{z}=a.\dfrac{z}{b}=\dfrac{a}{b}.z\left(\dfrac{a}{b}\text{ là hằng số vì a,b là các hằng số}\right)\)
Vậy x tỉ lệ thuận với z và hệ số tỉ lệ là \(\dfrac{a}{b}\)

a) Giả sử y tỉ lệ thuận với x theo hệ số tỉ lệ a nên y = a.x nên \(x = \dfrac{y}{a}\)
y tỉ lệ thuận với z theo hệ số tỉ lệ b nên y = b.z
Do đó, \(x = \dfrac{y}{a} = \dfrac{{b.z}}{a} = \dfrac{b}{a}.z\)( \(\dfrac{b}{a}\) là hằng số vì a,b là các hằng số)
Vậy x tỉ lệ thuận với z và hệ số tỉ lệ là \(\dfrac{b}{a}\)
b) Giả sử y tỉ lệ thuận với x theo hệ số tỉ lệ a nên y = a.x nên \(x = \dfrac{y}{a}\)
y tỉ lệ nghịch với z theo hệ số tỉ lệ b nên y = \(\dfrac{b}{z}\)
Do đó, \(x = \dfrac{y}{a} = \dfrac{{\dfrac{b}{z}}}{a} = \dfrac{b}{z}:a = \dfrac{b}{z}.\dfrac{1}{a} = \dfrac{{\dfrac{b}{a}}}{z}\)( \(\dfrac{b}{a}\) là hằng số vì a,b là các hằng số)
Vậy x tỉ lệ nghịch với z và hệ số tỉ lệ là \(\dfrac{b}{a}\)
c) Giả sử y tỉ lệ nghịch với x theo hệ số tỉ lệ a nên y = \(\dfrac{a}{x}\) nên x = \(\dfrac{a}{y}\)
y tỉ lệ nghịch với z theo hệ số tỉ lệ b nên y = \(\dfrac{b}{z}\)
Do đó, \(x = \dfrac{a}{y} = \dfrac{a}{{\dfrac{b}{z}}} = a:\dfrac{b}{z} = a.\dfrac{z}{b} = \dfrac{a}{b}.z\)( \(\dfrac{a}{b}\) là hằng số vì a,b là các hằng số)
Vậy x tỉ lệ thuận với z và hệ số tỉ lệ là \(\dfrac{a}{b}\)

Vì y tỉ lệ thuận với x theo hệ số tỉ lệ 4 3 nên y = 4 3 x
Vì x tỉ lệ nghịch với z theo tỉ lệ 6 7 nên x = 6 7 z
Thay x = 6 7 z vào y = 4 3 x ta được y = 4 3 . 6 7 z = 8 7 z hay y . z = 8 7
Do đó y và z tỉ lệ nghịch với nhau theo hệ số tỉ lệ 8 7
Đáp án cần chọn là B

* Bạn Hoa giải đúng.
* Bạn Hùng kết luận sai vì khi 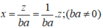 thì hai đại lượng x và z là hai đại lượng tỉ lệ thuận với hệ số tỉ lệ
thì hai đại lượng x và z là hai đại lượng tỉ lệ thuận với hệ số tỉ lệ 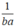

x = 4/y
z . \(-4\frac{1}{4}=y\)
x = 4/ z. \(-4\frac{1}{4}\)= -16/17 : z
Vay x ti le nghich voi z theo he so ti le -16/17

xy=2
=>y=2/x
y=5z
=>2/x=5z
=>xz=2/5
Vậy: x và z tỉ lệ nghịch theo hệ số tỉ lệ 2/5