BT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HP
13 tháng 8 2021
1.
a, Phương trình có nghiệm khi:
\(\left(m+2\right)^2+m^2\ge4\)
\(\Leftrightarrow m^2+4m+4+m^2\ge4\)
\(\Leftrightarrow2m^2+4m\ge0\)
\(\Leftrightarrow\left[{}\begin{matrix}m\ge0\\m\le-2\end{matrix}\right.\)
b, Phương trình có nghiệm khi:
\(m^2+\left(m-1\right)^2\ge\left(2m+1\right)^2\)
\(\Leftrightarrow2m^2+6m\le0\)
\(\Leftrightarrow-3\le m\le0\)
HP
13 tháng 8 2021
2.
a, Phương trình vô nghiệm khi:
\(\left(2m-1\right)^2+\left(m-1\right)^2< \left(m-3\right)^2\)
\(\Leftrightarrow4m^2-4m+1+m^2-2m+1< m^2-6m+9\)
\(\Leftrightarrow4m^2-7< 0\)
\(\Leftrightarrow-\dfrac{\sqrt{7}}{2}< m< \dfrac{\sqrt{7}}{2}\)
b, \(2sinx+cosx=m\left(sinx-2cosx+3\right)\)
\(\Leftrightarrow\left(m-2\right)sinx-\left(2m+1\right)cosx=-3m\)
Phương trình vô nghiệm khi:
\(\left(m-2\right)^2+\left(2m+1\right)^2< 9m^2\)
\(\Leftrightarrow m^2-4m+4+4m^2+4m+1< 9m^2\)
\(\Leftrightarrow m^2-1>0\)
\(\Leftrightarrow\left[{}\begin{matrix}m>1\\m< -1\end{matrix}\right.\)
CM
23 tháng 8 2017
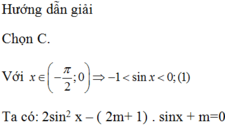
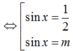
Phương trình sinx = 1/2 không có nghiệm x ∈ - π 2 ; 0
Nên để phương trình đã cho có nghiệm x ∈ - π 2 ; 0 khi và chỉ khi phương trình sinx = m có nghiệm trên khoảng đó. Kết hợp với (*) suy ra -1< m< 0
3P
1
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 10 2021
Do \(m^2-2m+1=\left(m-1\right)^2\ge0>-1;\forall m\) nên phương trình đã cho vô nghiệm khi:
\(m^2-2m+1>1\)
\(\Leftrightarrow m^2-2m>0\)
\(\Rightarrow\left[{}\begin{matrix}m>2\\m< 0\end{matrix}\right.\)
CM
6 tháng 7 2019
Chọn A.
y' = (m + 1)cosx – msinx – ( m + 2)
Phương trình y’ = 0 ⇔ (m + 1)cosx – msinx = (m + 2)
Điều kiện phương trình có nghiệm là a2 + b2 ≥ c2
⇔ (m + 1)2 + m2 ≥ (m + 2)2 ⇔ m2 – 2m – 3 ≥ 0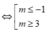 
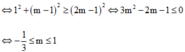
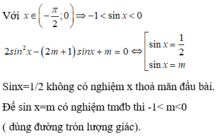
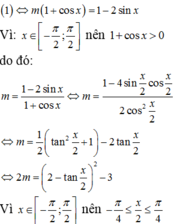
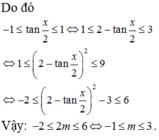
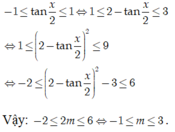
muốn giải bài này nhanh bạn cần biết đến công thức
PT:a.sinx +b.cosx =c có nghiệm khi:\(a^2+b^2\ge c^2\)
ADCT:\(\left(m-1\right)^2+m^2\ge3-2m\)
\(\Leftrightarrow m^2\ge1\)
\(\left[\begin{matrix}m\ge1\\m\le-1\end{matrix}\right.\)