
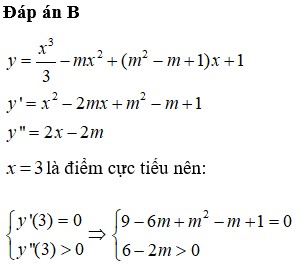
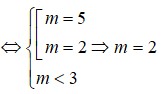
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

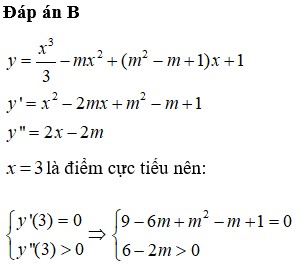
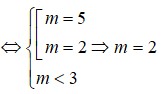

bước 1: ta tính y'
bước 2: giải pt y'=0 tìm ra xi
bước 3 tính y''
để hàm số có cực đại thì y''(xi)<0
đểhàm số có cực tiểu thì y''(xi)>0
giả các pt ta tìm đc điều kiện của m hàm số có cực đại, cực tiểu

ta có \(y'=4x^3+12mx^2+6\left(m+1\right)x\)
ta giải pt \(4x^3+12mx^2+6\left(m+1\right)x=0\Leftrightarrow x\left(4x^2+12mx+6m+6\right)=0\)
suy ra \(\begin{cases}x=0\\4x^2+12mx+6m+6=0\end{cases}\)
ta tính \(y''=12x^2+24mx+6m+6\)
để hàm số có cực đâị mà ko có cực tiểu thì y''(0)<0 với mọi x
giải pt suy ra đc điều kiện của m

Cho tam giác ABC đều
D thuộc AB , E thuộc AC sao cho BD = AE
CM : Khi D,E thay đổi ( di chuyển ) trên AB,AC thì đường trung tuyến DE luôn đi qua điểm cố định
Help me !!!

Đáp án là B
Ta có: y ' = 4 x 3 − 4 m x , y '' = 12 x 2 − 4 m .
Hàm số đã cho đạt cực tiểu tại x = − 1 nên y ' − 1 = 0 y ' ' − 1 > 0 ⇒ − 4 + 4 m = 0 12 + 4 m > 0 ⇔ m = 1.