Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

2: ΔABC vuông tại A nội tiếp (O)
=>O là trung điểm của BC
BC=căn 6^2+8^2=10cm
=>OB=OC=10/2=5cm
S=5^2*3,14=78,5cm2

Xét (O) có
\(\widehat{BAC}\) là góc nội tiếp chắn cung BC
Do đó: \(\widehat{BAC}=\dfrac{1}{2}\cdot\widehat{BOC}\)
=>\(\widehat{BOC}=75^0:\dfrac{1}{2}=150^0\)
Diện tích tam giác OBC là:
\(S_{OBC}=\dfrac{1}{2}\cdot OB\cdot OC\cdot sinBOC\)
\(=\dfrac{1}{2}\cdot1\cdot1\cdot sin150=\dfrac{1}{4}\)

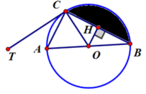
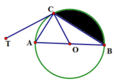
Ta có
T C A ^ = A B C ^ = 30 0 . cos A C B ^ = B C A B = 3 2 ⇒ B C = 3 c m .
Kẻ đường cao OH trong tam giác OBC. Ta có sin O B H ^ = O H O B = 1 2 ⇒ O H = 1 2 c m .
Diện tích tam giác OBC là s 1 = 1 2 . O H . B C = 3 4 c m 2 .
Ta có B O C ^ = 120 0 (vì O B C ^ = B C O ^ = 30 0 ).
Diện tích hình quạt chứa phần tô đen là s 2 = 120 360 . π . R 2 = π 3 c m 2 .
Diện tích phần tô đen là s = s 2 − s 1 = π 3 − 3 4 c m 2 .

Kiểm tra lại đề nha bạn. Chắc chắn là thiếu giả thiết rồi đó.
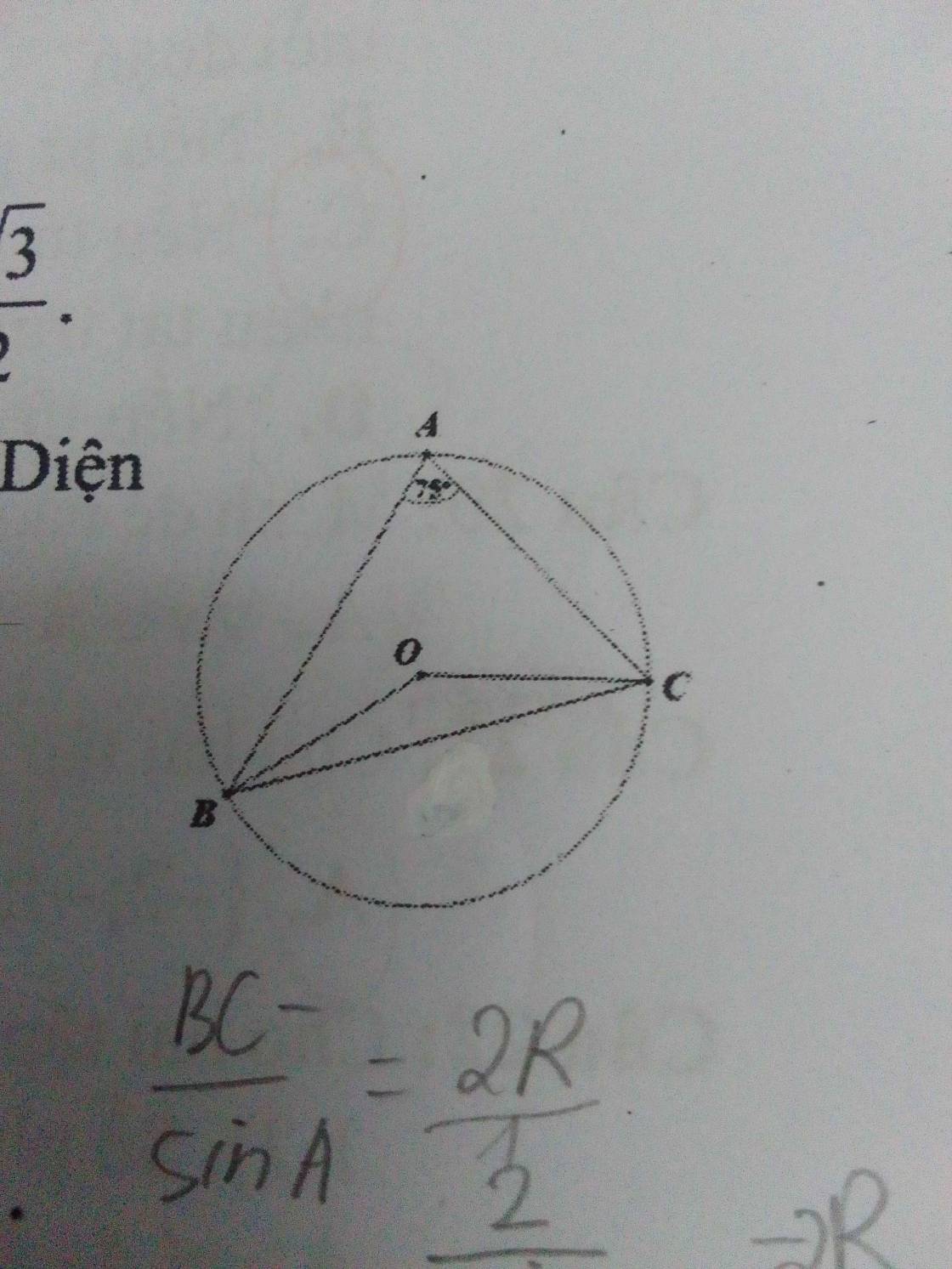
Vẽ tam giác thường ABC nội tiếp đường tròn tâm O bán kính r
Ta có diện tích tam giác đều nội tiếp đường tròn (O;r) có S =r23√34r2334
Gọi I là trung điểm cung BC có chứa A
Dựng OI vuông góc BC tại H và cắt (O;r) tại K
Ta có Diện tích tam giác ABC < diện tích tam giác BIC
S BCI = IH.HB
S2BIC=HB2.IH2SBIC2=HB2.IH2
Lại có: BH2=HK.HIBH2=HK.HI (Hệ thức lượng)
Do đóS2BIC=KH.IH3=(2r−IH)IH3=IH33(6r−3IH)SBIC2=KH.IH3=(2r−IH)IH3=IH33(6r−3IH)
Áp dụng BĐT AM-GM ta có
HI+HI+HI+(6r−3HI)≥44√HI3.(6r−3IH)⇔32r≥44√HI3.(6r−3IH)HI+HI+HI+(6r−3HI)≥4HI3.(6r−3IH)4⇔32r≥4HI3.(6r−3IH)4
⇒8116r4≥IH3(6r−3IH)⇔2716r2≥IH3.(2r−IH)⇒3√34R2≥√IH3(2r−IH)=SBIC⇒8116r4≥IH3(6r−3IH)⇔2716r2≥IH3.(2r−IH)⇒334R2≥IH3(2r−IH)=SBIC
Do đóSABCSABC
Dấu "=" xảy ra khi HI = 6r -3IH
Do đó HI =32r32r
Vẽ tam giác thường ABC nội tiếp đường tròn tâm O bán kính r
Ta có diện tích tam giác đều nội tiếp đường tròn (O;r) có S =r23√34r2334
Gọi I là trung điểm cung BC có chứa A
Dựng OI vuông góc BC tại H và cắt (O;r) tại K
Ta có Diện tích tam giác ABC < diện tích tam giác BIC
S BCI = IH.HB
S2BIC=HB2.IH2SBIC2=HB2.IH2
Lại có: BH2=HK.HIBH2=HK.HI (Hệ thức lượng)
Do đóS2BIC=KH.IH3=(2r−IH)IH3=IH33(6r−3IH)SBIC2=KH.IH3=(2r−IH)IH3=IH33(6r−3IH)
Áp dụng BĐT AM-GM ta có
HI+HI+HI+(6r−3HI)≥44√HI3.(6r−3IH)⇔32r≥44√HI3.(6r−3IH)HI+HI+HI+(6r−3HI)≥4HI3.(6r−3IH)4⇔32r≥4HI3.(6r−3IH)4
⇒8116r4≥IH3(6r−3IH)⇔2716r2≥IH3.(2r−IH)⇒3√34R2≥√IH3(2r−IH)=SBIC⇒8116r4≥IH3(6r−3IH)⇔2716r2≥IH3.(2r−IH)⇒334R2≥IH3(2r−IH)=SBIC
Do đóSABCSABC
Dấu "=" xảy ra khi HI = 6r -3IH
Do đó HI =32r32r
Vẽ tam giác thường ABC nội tiếp đường tròn tâm O bán kính r
Ta có diện tích tam giác đều nội tiếp đường tròn (O;r) có S =r23√34r2334
Gọi I là trung điểm cung BC có chứa A
Dựng OI vuông góc BC tại H và cắt (O;r) tại K
Ta có Diện tích tam giác ABC < diện tích tam giác BIC
S BCI = IH.HB
S2BIC=HB2.IH2SBIC2=HB2.IH2
Lại có: BH2=HK.HIBH2=HK.HI (Hệ thức lượng)
Do đóS2BIC=KH.IH3=(2r−IH)IH3=IH33(6r−3IH)SBIC2=KH.IH3=(2r−IH)IH3=IH33(6r−3IH)
Áp dụng BĐT AM-GM ta có
HI+HI+HI+(6r−3HI)≥44√HI3.(6r−3IH)⇔32r≥44√HI3.(6r−3IH)HI+HI+HI+(6r−3HI)≥4HI3.(6r−3IH)4⇔32r≥4HI3.(6r−3IH)4
⇒8116r4≥IH3(6r−3IH)⇔2716r2≥IH3.(2r−IH)⇒3√34R2≥√IH3(2r−IH)=SBIC⇒8116r4≥IH3(6r−3IH)⇔2716r2≥IH3.(2r−IH)⇒334R2≥IH3(2r−IH)=SBIC
Do đóSABCSABC
Dấu "=" xảy ra khi HI = 6r -3IH
Do đó HI =32r32r
chưa đọc mà đã thấy hoa mắt rồi bn ơi