Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Câu 1: đáp án C đúng (đáp án A và B hiển nhiên sai, đáp án D chỉ đúng khi a không âm)
Câu 2: (I) sai, vì với \(x< -1\) hàm ko xác định nên ko liên tục
(II) đúng do tính chất hàm sin
(III) đúng do \(\lim\limits_{x\rightarrow1}\frac{\left|x\right|}{x}=\frac{\left|1\right|}{1}=f\left(1\right)\)
Vậy đáp án D đúng
+) Ta có (I) đúng vì f ( x ) = x 5 - x 2 + 1 là hàm đa thức nên liên tục trên R
+) Ta có (III) đúng vì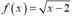 
liên tục trên (2;+∞) và 
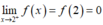nên hàm số liên tục trên [2;+∞).
+) (II) sai vì trên khoảng ( -1, 1)hàm số đã cho không xác định nên hàm số không liên tục trên khoảng đó.
Chọn D
a) Các bạn tự vẽ hình nhé . Đồ thị hàm số y = f(x) là một đường không liền nét mà bị đứt quãng tại x0 = -1. Vậy hàm số đã cho liên tục trên khoảng (-∞; -1) và (- 1; +∞).
b) +) Nếu x < -1: f(x) = 3x + 2 liên tục trên (-∞; -1) (vì đây là hàm đa thức).
+) Nếu x> -1: f(x) = x2 – 1 liên tục trên (-1; +∞) (vì đây là hàm đa thức).
+) Tại x = -1;
Ta có =
= 3(-1) +2 = -1.
= (-1)2 – 1 = 0.
Vì 
nên không tồn tại 
. Vậy hàm số gián đoạn tại
x0 = -1.
TenAnh1 TenAnh1 A = (-0.04, -7.12) A = (-0.04, -7.12) A = (-0.04, -7.12) B = (15.32, -7.12) B = (15.32, -7.12) B = (15.32, -7.12) D = (10.58, -5.6) D = (10.58, -5.6) D = (10.58, -5.6)
+) Hàm số 
xác định khi và chỉ khi x2+ x – 6 ≠ 0 <=> x ≠ -3 và x ≠ 2.
Hàm số f(x) liên tục trên các khoảng (-∞; -3), (-3; 2) và (2; +∞)
+) Hàm số g(x) = tanx + sinx xác định khi và chỉ khi
tanx ≠ 0 <=> x ≠ π/2 +kπ với k ∈ Z.
Hàm số g(x) liên tục trên các khoảng ( – π/2+kπ; π/2 +kπ) với k ∈ Z.
Chọn B.
Ta có (II) đúng vì hàm số lượng giác liên tục trên từng khoảng của tập xác định.
Ta có (III) đúng vì 
Khi đó 
Vậy hàm số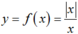 
liên tục tại x = 1.
Tham khảo:
Xét hàm số g(x) = f(x) − f(x + 0,5)
Ta có
g(0) = f(0) − f(0 + 0,5) = f(0) − f(0,5)
g(0,5) = f(0,5) − f(0,5 + 0,5) = f(0,5) − f(1) = f(0,5) − f(0)
(vì theo giả thiết f(0) = f(1)).
Do đó,
- Ta có (II) đúng vì hàm số lượng giác liên tục trên từng khoảng của tập xác định.
- Ta có (III) đúng vì
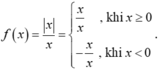
- Khi đó:
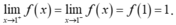
- Vậy hàm số
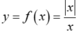
liên tục tại x = 1.
- (I) Sai vì với x < -1 thì hàm số đã cho không xác định nên tại các điểm x 0 < - 1 thì hàm số đã cho không liên tục.
Chọn D.
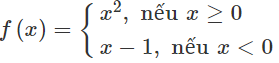
Chọn D.
Ta có (I) đúng vì f(x) = x5 – x2 + 1 là hàm đa thức nên liên tục trên R..
Ta có (III) đúng vì
liên tục trên (2; +∞) và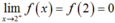 
nên hàm số liên tục trên [2; +∞)
(!!) sai vì hàm số gián đoạn tại các điểm hàm số không xác định.