Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi hai số cần tìm là x, y.
Theo đề bài ta có:
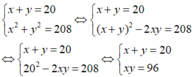
Suy ra x, y là nghiệm của phương trình:
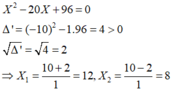
Vậy hai số cần tìm là 12 và 8

Gọi 2 số là a và b (a,b....)
Theo bài ta có:
\(\hept{\begin{cases}a+b=23\\\left(a-b\right)^2=23\end{cases}}\Rightarrow\hept{\begin{cases}a=23-b\\\left(a-b\right)^2=23\end{cases}}\)
\(\Rightarrow\left(23-b-b\right)^2=23\)\(\Rightarrow b=....\)
\(\Rightarrow a=23-b=23-....\)

Vậy 2 số cần tìm là 8 và 11Gọi 2 số tự nhiên cần tìm là a,b (a>b)
Theo giả thiết, ta có
a + b = 19 và a^2 + b^2 = 185
=> 2ab = (a+b)^2 - (a^2+b^2) = 176 <=> ab = 88
=> a,b là nghiệm của pt x^2 - 19x + 88 = 0 (*)
(*) <=> (x-11)(x-8) = 0 <=> x= 8 hoặc x = 11
=> (a,b) = (11;8)
gọi x là số tự nhiên thứ nhất , y là số tự nhiên thứ hai . (x,y > 0)
tổng của chúng bằng 19
=> x + y = 19
<=> x = 19 - y
tổng các bình phương của chúng bằng 185
=> x^2 + y^2 = 185
<=> (19 - y)^2 + y^2 = 185
<=> 361 - 38y + y^2 + y^2= 185
<=> 2y^2 - 38y + 176 = 0
<=> y = 8 hoặc y = 11
y = 8 => x = 19 - 8 = 11
y = 11 => x = 19 - 11 = 8
vậy hai số tự nhiên đó là 8 và 11

theo bài ra ta có hệ pt:
a+b=5
a^2+b^2=13
giai he pt ra ta dc b=2hoacb=3

ab
trong hệ tp ab=10a+b
theo bài có pt
10a+b=a^2+b^2-11
10a+b=2a.b+5
giải hệ trên
với 0<a<=9, 0<=b<=9
(1-2)=>(a-b)^2=16=>a-b=+-4
=>b=a+-4
thay vào (2)
10a+a+-4=2a^2+-8+5
2a^2-11a+-4+5=0
•2a^2-11a+1=0 loại a không nguyên
•2a^2-11a+9=0
a=(11+-7)/4
a=18/4 loại
a=1 nhận
b=5
đáp số: 15

Gọi số thứ nhất là x
\(\Rightarrow\)Số thứ hai là 19-x
Theo đề bài ta có phương trình:
x2+(19-x)2=185
\(\Leftrightarrow x^2+361-38x+x^2=185\)
\(\Leftrightarrow2x^2-38x+361-185=0\)
\(\Leftrightarrow2x^2-38x+176=0\)
\(\Leftrightarrow x^2-19x+88=0\)
\(\Leftrightarrow x^2-11x-8x+88=0\)
\(\Leftrightarrow x\left(x-11\right)-8\left(x-11\right)=0\)
\(\Leftrightarrow\left(x-11\right)\left(x-8\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x-11=0\\x-8=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=11\\x=8\end{cases}}\)
Vậy số thứ nhất là 8, số thứ hai là 19-8=11 hoặc số thứ nhất là 11, số thứ hai là 19-11=8
Gọi số thứ nhất là x. Như vậy thì số thứ hai là 20-x.
Ta có phương trình \(x^2+\left(20-x\right)^2=280\Leftrightarrow2x^2-40x+120=0\Leftrightarrow x^2-20x+60=0\Rightarrow x=10\pm2\sqrt{10}\)
Vậy hai số đó là \(10+2\sqrt{10}\)và\(10-2\sqrt{10}\)