Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì hai số có tổng bằng 10 và tích bằng -10 nên nó là nghiệm của phương trình: x 2 – 10x – 10 = 0
Ta có: ∆ ' = - 5 2 – 1.(-10) = 25 + 10 = 35 > 0
∆ ' = 35
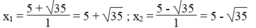
Vậy hai số đó là 5 + 35 và 5 - 35

Số bé là:
(24 - 10) : 2 = 7
Số lớn là:
7+10=17

Hai số cần tìm là nghiệm của phương trình x2 - x + 5 = 0
Δ = b2 - 4ac = (-1)2 - 4.1.5 = -19 < 0
⇒ phương trình vô nghiêm
Vậy không tồn tại 2 số có tổng bằng 1 và tích bằng 5

Hai số cần tìm là nghiệm của phương trình x 2 - x + 5 = 0
Δ = b 2 - 4 a c = ( - 1 ) 2 - 4 . 1 . 5 = - 19 < 0
⇒ phương trình vô nghiêm
Vậy không tồn tại 2 số có tổng bằng 1 và tích bằng 5

Bài 1:
Gọi hai số tự nhiên cần tìm là a,b
Số thứ nhất gấp 4 lần số thứ hai nên a=4b(1)
Tổng của hai số là 100 nên a+b=100(2)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}a=4b\\a+b=100\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}4b+b=100\\a=4b\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5b=100\\a=4b\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}b=\dfrac{100}{5}=20\\a=4\cdot20=80\end{matrix}\right.\)
Bài 2:
Gọi hai số cần tìm là a,b
Hiệu của hai số là 10 nên a-b=10(4)
Hai lần số thứ nhất bằng ba lần số thứ hai nên 2a=3b(3)
Từ (3) và (4) ta có hệ phương trình:
\(\left\{{}\begin{matrix}a-b=10\\2a=3b\end{matrix}\right.\Leftrightarrow\)\(\left\{{}\begin{matrix}a-b=10\\2a-3b=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2a-2b=20\\2a-3b=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2a-2b-2a+3b=20\\2a=3b\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=20\\2a=3\cdot20=60\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}a=30\\b=20\end{matrix}\right.\)
Bài 3:
Gọi số tự nhiên cần tìm có dạng là \(\overline{ab}\left(a\ne0\right)\)
Chữ số hàng chục bé hơn chữ số hàng đơn vị là 3 nên b-a=3(5)
Nếu đổi chỗ hai chữ số cho nhau thì tổng của số mới lập ra và số ban đầu là 77 nên ta có:
\(\overline{ab}+\overline{ba}=77\)
=>\(10a+b+10b+a=77\)
=>11a+11b=77
=>a+b=7(6)
Từ (5) và (6) ta có hệ phương trình:
\(\left\{{}\begin{matrix}-a+b=5\\a+b=7\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-a+b+a+b=5+7\\a+b=7\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2b=12\\a+b=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=6\\a=7-6=1\end{matrix}\right.\)
Vậy: Số tự nhiên cần tìm là 16
tìm 2 số có : tổng = 10 và tích = -10
2 số đó là nghiệm của phương trình
x2- 10x - 10 = 0
\(\Delta\) = (-10)2-4.1.(-10) = 100 + 40 = 140 > 0
\(\Rightarrow\) phương trình có 2 nghiệm phân biệt
x1= \(\dfrac{10+\sqrt{140}}{2}\) =5 + \(\sqrt{35}\)
x2=\(\dfrac{10-\sqrt{140}}{2}\) =5 - \(\sqrt{35}\)
vậy 2 số đó là :5 + \(\sqrt{35}\) và 5 - \(\sqrt{35}\)