
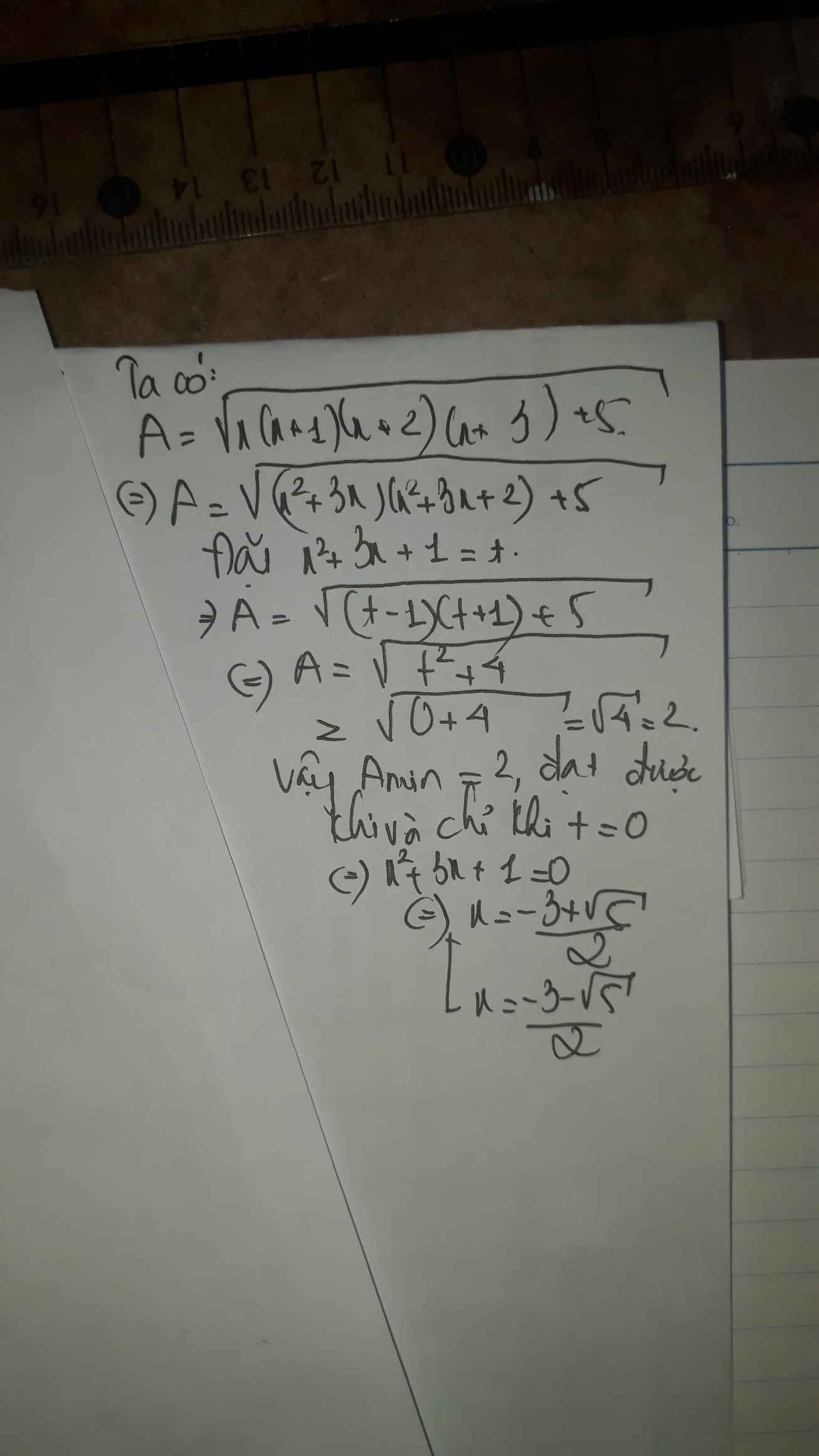
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

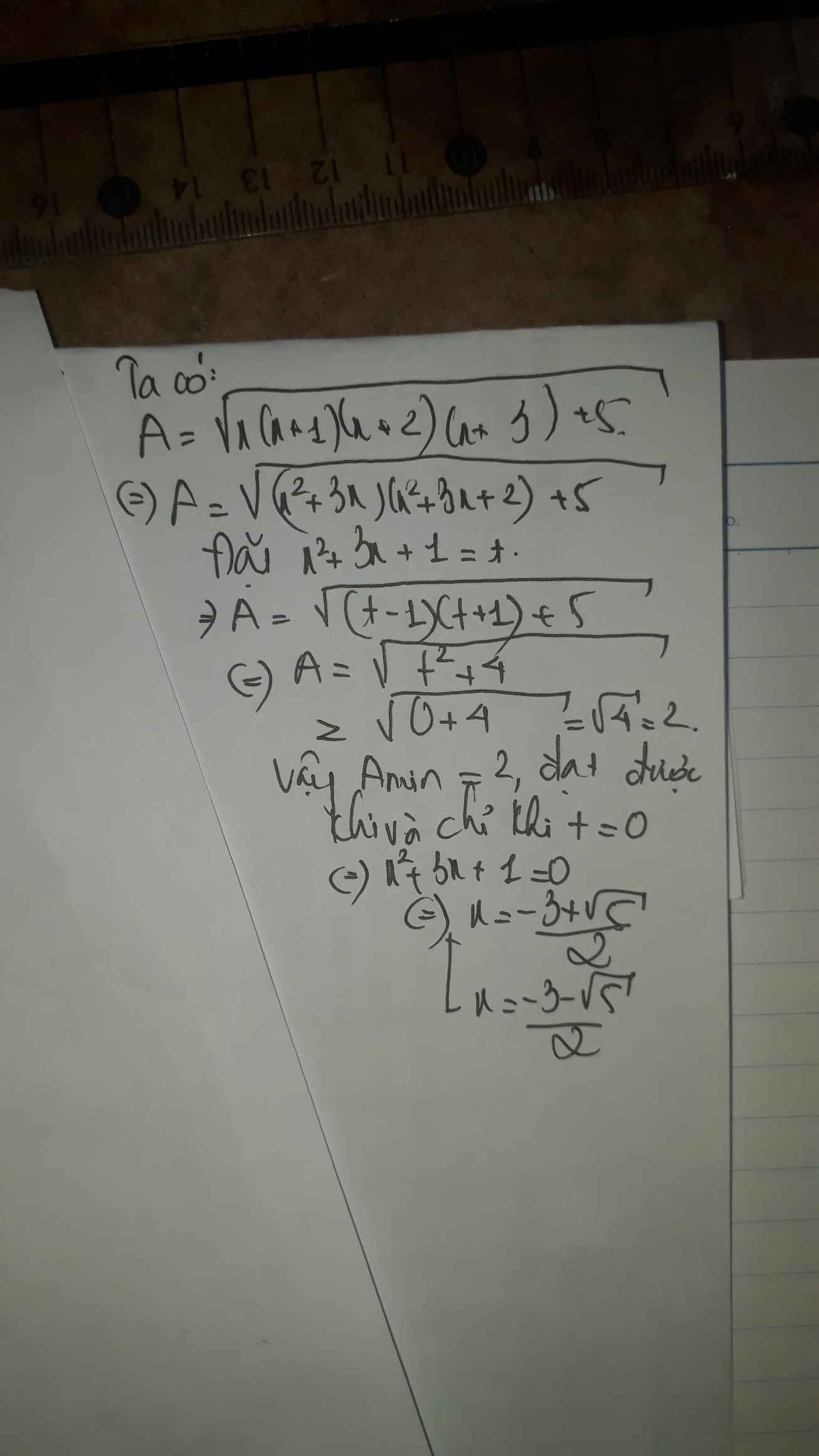

Đặt \(F=\sqrt{x\left(x+1\right)\left(x+2\right)\left(x+3\right)+5}\)
\(=\sqrt{\left(x^2+3x\right)\left(x^2+3x+2\right)+5}\left(#\right)\)
# đặt \(t=x^2+3x\) ta có
\(\left(#\right)=\sqrt{t\cdot\left(t+2\right)+5}=\sqrt{\left(t+1\right)^2+4}\)
(#) đạt giá trị nhỏ nhất của F=2 khi t+1=0 hay t=-1
Vậy \(F_{min}=2\) khi \(x=\frac{-3\pm\sqrt{5}}{2}\)

Bài 1:
\(P=x\sqrt{3-x^2}=\sqrt{x^2}\cdot\sqrt{3-x^2}\)
\(=\sqrt{x^2\left(3-x^2\right)}\)\(\le\frac{x^2+3-x^2}{2}=\frac{3}{2}\)
Dấu = khi \(x=\sqrt{\frac{3}{2}}\)
Vậy MaxP=\(\frac{3}{2}\Leftrightarrow x=\sqrt{\frac{3}{2}}\)

\(A=\left(x-1\right)\left(x-8\right)\left(x-4\right)\left(x-5\right)+2002\)
\(\Leftrightarrow A=\left(x^2-9x+8\right)\left(x^2-9x+20\right)+2002\)
Đặt \(x^2-9x+14=y\)
\(\Rightarrow A=\left(y-6\right)\left(y+6\right)+2002\)
\(\Leftrightarrow A=y^2-36+2002\)
\(\Leftrightarrow A=y^2+1966\ge1966\)
Dấu "=" xảy ra khi
\(x^2-9x+14=0\)
\(\Leftrightarrow x=2,7\)

Áp dụng BĐT AM-GM ta có:
\(\frac{\left(x+1\right)\left(y+1\right)^2}{3\sqrt[3]{x^2y^2}+1}\ge\frac{\left(x+1\right)\left(y+1\right)^2}{xy+x+y+1}=\frac{\left(x+1\right)\left(y+1\right)^2}{\left(x+1\right)\left(y+1\right)}=y+1\)
Tương tự cho 2 BĐT còn lại rồi cộng theo vế:
\(P\ge x+y+z+3=6\)
Dấu "=" <=> x=y=z=1

\(A=\sqrt{\left(x-2\right)\left(x-1\right)x\left(x+1\right)+5}\)
\(=\sqrt{\left(x^2-x-2\right)\left(x^2-x\right)+5}\)
Đặt \(t=x^2-x\) ta đc:
\(A=\sqrt{\left(t-2\right)t+5}=\sqrt{t^2-2t+5}\)
\(=\sqrt{\left(t-1\right)^2+4}\ge\sqrt{4}=2\)
Dấu = khi \(t=1\Leftrightarrow x^2-x=1\Leftrightarrow x=\pm\frac{1}{2}+\frac{\sqrt{5}}{2}\)
Vậy....
b)\(B=\sqrt{x^2-4x+4}+\sqrt{x^2+6x+9}\)
\(=\sqrt{\left(x-2\right)^2}+\sqrt{\left(x+3\right)^2}\)
\(=\left|x-2\right|+\left|x+3\right|\)
Áp dụng Bđt \(\left|a\right|+\left|b\right|\ge\left|a+b\right|\) ta có:
\(\left|x-2\right|+\left|x+3\right|=\left|x-2\right|+\left|-x-3\right|\ge\left|x-2+\left(-x\right)-3\right|=5\)
Dấu = khi \(\left(x-2\right)\left(x+3\right)\ge0\)\(\Rightarrow-3\le x\le2\)
\(\Rightarrow\hept{\begin{cases}-3\le x\le2\\\left(x+3\right)\left(x-2\right)=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=-3\\x=2\end{cases}}\)
Vậy....

a,\(A\ge\frac{9}{\sqrt{x}+\sqrt{y}+\sqrt{z}}\ge\frac{9}{\sqrt{3\left(x+y+z\right)}}=3\)=3
MInA=3<=>x=y=z=1
b)dùng cô si đi(đề thi chuyên bình phước năm 2016-2017)

\(F=\sqrt{x\left(x+1\right)\left(x+2\right)\left(x+3\right)+5}=\sqrt{\left(x^2+3x\right)\left(x^2+3x+2\right)+5}\) ( * )
*Đặt \(t=x^2+3x\)Ta có :
( * ) \(=\sqrt{t.\left(t+2\right)+5}=\sqrt{\left(t+1\right)^2+4}\)
( * ) Đạt GTNN của F khi bằng 2 khi \(t+1=0\) hay \(t=-1\)
Vậy \(^{minF=2\Leftrightarrow x=\frac{-3\pm\sqrt{5}}{2}}\)

A = \(\sqrt{\left(x-3\right)-2\sqrt{x-3}+1+2}\)
= \(\sqrt{\left(\sqrt{x-3}-1\right)^2+2}\)\(\ge\)\(\sqrt{0+2}\)=\(\sqrt{2}\)
''='' <=> x = 4
=> Min A = \(\sqrt{2}\)và x = 4
B = |x-2011| + |x-1|
TH1: x \(\le\)1
=> B = 2012 - 2x \(\ge\)2010 ''='' <=> x = 1
TH2: 1\(\le\)x\(\le\)2011
=> B = x - 1 + 2011 - x = 2010 với mọi x t/m đkiện
TH3: x \(\ge\)2011
=> B = 2x - 2012 \(\ge\)2010 ''='' <=> x = 2011
Vậy Min B = 2010 <=> 1\(\le\)x\(\le\)2011

a) \(A=\sqrt{x^2-2x+1}+\sqrt{x^2-6x+9}\)
\(=\sqrt{\left(x-1\right)^2}+\sqrt{\left(x-3\right)^2}\)
\(=\left|x-1\right|+\left|x-3\right|\ge\left|\left(x-1\right)+\left(3-x\right)\right|=2\)
Vậy\(A_{min}=2\Leftrightarrow\left(x-1\right)\left(3-x\right)\ge0\)
\(TH1:\hept{\begin{cases}x-1\ge0\\3-x\ge0\end{cases}}\Leftrightarrow1\le x\le3\)
\(TH1:\hept{\begin{cases}x-1\le0\\3-x\le0\end{cases}}\Leftrightarrow\hept{\begin{cases}x\le1\\x\ge3\end{cases}}\left(L\right)\)
Vậy \(A_{min}=2\Leftrightarrow1\le x\le3\)

từ dòng cuối là sai rồi bạn à
Bạn bỏ dòng cuối đi còn lại đúng rồi
Ở tử đặt nhân tử chung căn x chung rồi lại đặt căn x +1 chung
Ở mẫu tách 3 căn x ra 2 căn x +căn x rồi đặt nhân tử 2 căn x ra
rút gọn được \(\frac{3\sqrt{x}-5}{2\sqrt{x}+1}\)