N
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PT
2
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 3 2020
\(A=x^4+6x^3+9x^2+4x^2+12x+12\)
\(=\left(x^2+3x\right)^2+4\left(x^2+3x\right)+4+8\)
\(=\left(x^2+3x+2\right)^2+8\ge8\)
Dấu "=" xảy ra khi \(\left[{}\begin{matrix}x=-1\\x=-2\end{matrix}\right.\)
3 tháng 2 2022
a: \(A=\left(\dfrac{2\left(2x+1\right)}{2\left(2x+4\right)}-\dfrac{x}{3x-6}-\dfrac{2x^3}{3x^3-12x}\right):\dfrac{6x+13x^2}{24x-12x^2}\)
\(=\left(\dfrac{2x+1}{2\left(x+2\right)}-\dfrac{x}{3\left(x-2\right)}-\dfrac{2x^3}{3x\left(x^2-4\right)}\right):\dfrac{x\left(13x+6\right)}{x\left(24-12x\right)}\)
\(=\left(\dfrac{2x+1}{2\left(x+2\right)}-\dfrac{x}{3\left(x-2\right)}-\dfrac{2x^2}{3\left(x-2\right)\left(x+2\right)}\right):\dfrac{13x+6}{-12\left(x-2\right)}\)
\(=\dfrac{3\left(2x+1\right)\left(x-2\right)-2x\left(x+2\right)-4x^2}{6\left(x+2\right)\left(x-2\right)}\cdot\dfrac{-12\left(x-2\right)}{13x+6}\)
\(=\dfrac{3\left(2x^2-3x-2\right)-2x^2-4x-4x^2}{x-2}\cdot\dfrac{-2}{13x+6}\)
\(=\dfrac{6x^2-9x-6-6x^2-4x}{x-2}\cdot\dfrac{-2}{13x+6}\)
\(=\dfrac{-\left(13x+6\right)\cdot\left(-2\right)}{\left(13x+6\right)\left(x-2\right)}=\dfrac{2}{x-2}\)
b: Để A>0 thì x-2>0
hay x>2
Để A>-1 thì A+1>0
\(\Leftrightarrow\dfrac{2+x-2}{x-2}>0\)
=>x/x-2>0
=>x>2 hoặc x<0
TT
0
TT
2
19 tháng 12 2016
Đề sai một chút nha bạn : mình sửa bạn thử tham khảo xem đúng không \(P=\frac{12x^2-6x+4}{\left(x-1\right)^2}\)
Mình làm luôn nha
Giải
Theo bài ra , ta có :
\(P=\frac{12x^2-6x+4}{\left(x-1\right)^2}=\frac{12\left(x^2-2x+1\right)+18x-8+10x-10+10}{\left(x-1\right)^2}=\frac{12\left(x-1\right)^2+18\left(x-1\right)+10}{\left(x-1\right)^2}=12+\frac{18}{x-1}+\frac{10}{\left(x-1\right)^2}\)
Đặt \(\frac{2}{x-1}=y\)
Đến đây bạn tự làm tiếp nhé
MT
7 tháng 10 2019
a) \(x^2+6x-3\)
\(=x^2+6x+9-12\)
\(=\left(x+3\right)^2-12\ge-12\)
Vậy GTNN của bt là -12\(\Leftrightarrow x+3=0\Leftrightarrow x=-3\)
HN
11 tháng 12 2017
a/ \(\left(a^2+b^2\right)+\left(a^2+1\right)+\left(b^2+1\right)\ge2ab+2a+2b\)
\(\Leftrightarrow a^2+b^2+1\ge ab+a+b\)
b/ \(\dfrac{1}{a}+\dfrac{1}{b}\ge\dfrac{4}{a+b}\)
\(\Leftrightarrow a^2-2ab+b^2\ge0\)
\(\Leftrightarrow\left(a-b\right)^2\ge0\) đúng
c/ \(M=x^4-6x^3+13x^2-12x-5\)
Đặt \(x^2-3x=a\)thì ta có:
\(M=a^2+4a-5=\left(a+2\right)^2-9\ge-9\)
Dấu = xảy ra khi:
\(x^2-3x+2=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=2\end{matrix}\right.\)
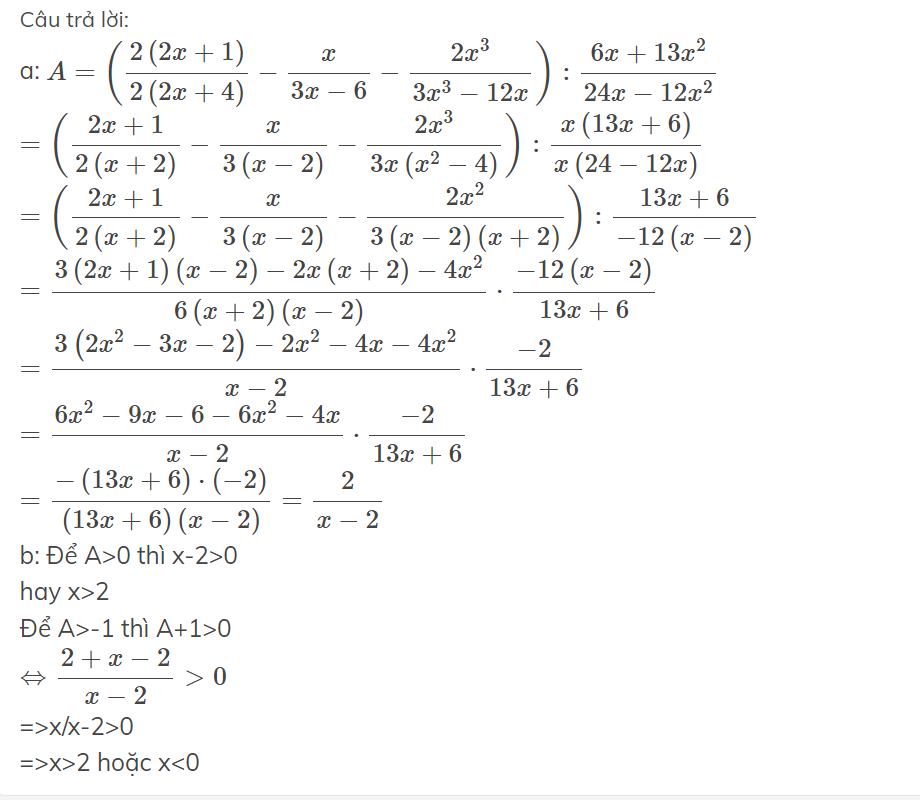
\(A=x^4+6x^3+13x^2+12x+12\)
\(=\left(x^4+6x^3+19x^2+30x+25\right)-6x^2-18x-30+17\)
\(=\left(x^4+6x^3+19x^2+30x+25\right)-6\left(x^2+3x+5\right)+17\)
\(=\left(x^2+3x+5\right)^2-6\left(x^2+3x+5\right)+17\)
Đặt \(t=x^2+3x+5\)
Khi đó \(A=t^2-6t+17=t^2-2.t.3+9+8=\left(t-3\right)^2+8\ge8\)
Dấu "=" xảy ra <=> t - 3 = 0 <=> t = 3
<=> \(x^2+3x+5=3\Leftrightarrow x^2+3x+2=0\)
\(\Leftrightarrow x^2+x+2x+2=0\)
\(\Leftrightarrow x\left(x+1\right)+2\left(x+1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=-1\\x=-2\end{cases}}\)
Vậy AMin = 8 khi và chỉ khi x = -1 hoặc x = -2
CÁC BẠN GIẢI NHANH HỘ NHÚN VỚI