Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(0< \alpha< 90^o\)
b) \(90^o< \alpha< 180^o\)
c) \(0< \alpha< 90^o\)
d) \(90^o< \alpha< 180^o\)

a/ \(\frac{\pi}{2}\le y\le\pi\Rightarrow cosy< 0\)
\(\Rightarrow cosy=-\sqrt{1-sin^2y}=-\frac{2\sqrt{2}}{3}\)
\(sin2y=2siny.cosy=2.\left(\frac{1}{3}\right).\left(-\frac{2\sqrt{2}}{3}\right)=-\frac{4\sqrt{2}}{9}\)
\(cos\left(\frac{\pi}{3}-y\right)=cos\frac{\pi}{3}cosy+sin\frac{\pi}{3}siny=\frac{\sqrt{3}-2\sqrt{2}}{6}\)
\(tany+5=\frac{siny}{cosy}+5=5-\frac{\sqrt{2}}{4}\)
b/ \(-\frac{\pi}{2}\le a\le9\Rightarrow sina\le0\)
\(\Rightarrow sina=\sqrt{1-cos^2a}=-\frac{4}{5}\)
\(sin2a=2sina.cosa=-\frac{24}{25}\)
\(cos2a=cos^2a-sin^2a=-\frac{7}{25}\)
\(tan2a=\frac{sin2a}{cos2a}=\frac{24}{7}\)
c/ \(\pi\le a\le\frac{3\pi}{2}\Rightarrow\left\{{}\begin{matrix}sina\le0\\cosa\le0\end{matrix}\right.\)
\(\Rightarrow cosa=-\frac{1}{\sqrt{1+tan^2a}}=-\frac{1}{2}\Rightarrow sina=-\frac{\sqrt{3}}{2}\)
\(\Rightarrow sin2a=2sina.cosa=\frac{\sqrt{3}}{2}\)
\(\Rightarrow\left(\sqrt{3}-sin2a\right)sin\frac{2\pi}{3}=\frac{3}{4}\)

\(sina\sqrt{1+\frac{sin^2a}{cos^2a}}=sina\sqrt{\frac{cos^2a+sin^2a}{cos^2a}}=\frac{sina}{\left|cosa\right|}=\pm tana\)
\(\frac{1-cos^2x}{1-sin^2x}+tanx.cotx=\frac{sin^2x}{cos^2x}+\frac{sinx}{cosx}.\frac{cosx}{sinx}=tan^2x+1=\frac{1}{cos^2x}\)
\(\frac{1-4sin^2xcos^2x}{\left(sinx+cosx\right)^2}=\frac{\left(1-2sinx.cosx\right)\left(1+2sinx.cosx\right)}{sin^2x+cos^2x+2sinx.cosx}=\frac{\left(1-sin2x\right)\left(1+2sinx.cosx\right)}{1+2sinx.cosx}=1-2sinx\)
\(sin\left(90-x\right)+cos\left(180-x\right)+sin^2x\left(1+tan^2x\right)-tan^2x\)
\(=cosx-cosx+sin^2x.\frac{1}{cos^2x}-tan^2x=tan^2x-tan^2x=0\)

a/
\(\frac{1}{sinx}+\frac{cosx}{sinx}=\frac{1+cosx}{sinx}=\frac{1+2cos^2\frac{x}{2}-1}{2sin\frac{x}{2}cos\frac{x}{2}}=\frac{2cos^2\frac{x}{2}}{2sin\frac{x}{2}cos\frac{x}{2}}=\frac{cos\frac{x}{2}}{sin\frac{x}{2}}=cot\frac{x}{2}\)
b/
\(\frac{1-cosx}{sinx}=\frac{1-\left(1-2sin^2\frac{x}{2}\right)}{2sin\frac{x}{2}cos\frac{x}{2}}=\frac{2sin^2\frac{x}{2}}{2sin\frac{x}{2}cos\frac{x}{2}}=\frac{sin\frac{x}{2}}{cos\frac{x}{2}}=tan\frac{x}{2}\)
c/
\(tan\frac{x}{2}\left(\frac{1}{cosx}+1\right)=\left(\frac{1-cosx}{sinx}\right)\left(\frac{1}{cosx}+1\right)=\frac{\left(1-cosx\right)\left(1+cosx\right)}{sinx.cosx}=\frac{1-cos^2x}{sinx.cosx}\)
\(=\frac{sin^2x}{sinx.cosx}=\frac{sinx}{cosx}=tanx\)
d/
\(\frac{sin2a}{2cosa\left(1+cosa\right)}=\frac{2sina.cosa}{2cosa\left(1+2cos^2\frac{a}{2}-1\right)}=\frac{sina}{2cos^2\frac{a}{2}}=\frac{2sin\frac{a}{2}cos\frac{a}{2}}{2cos^2\frac{a}{2}}=tan\frac{a}{2}\)
e/
\(cotx+tan\frac{x}{2}=\frac{cosx}{sin}+\frac{1-cosx}{sinx}=\frac{cosx+1-cosx}{sinx}=\frac{1}{sinx}\)
Các câu c, e đều sử dụng kết quả từ câu b
f/
\(3-4cos2x+cos4x=3-4cos2x+2cos^22x-1\)
\(=2cos^22x-4cos2x+2=2\left(cos^22x-2cos2x+1\right)\)
\(=2\left(cos2x-1\right)^2=2\left(1-2sin^2x-1\right)^2\)
\(=2.\left(-2sin^2x\right)^2=8sin^4x\)
g/
\(\frac{1-cosx}{sinx}=\frac{sinx\left(1-cosx\right)}{sin^2x}=\frac{sinx\left(1-cosx\right)}{1-cos^2x}=\frac{sinx\left(1-cosx\right)}{\left(1-cosx\right)\left(1+cosx\right)}=\frac{sinx}{1+cosx}\)
h/
\(sinx+cosx=\sqrt{2}\left(sinx.\frac{\sqrt{2}}{2}+cosx.\frac{\sqrt{2}}{2}\right)\)
\(=\sqrt{2}\left(sinx.cos\frac{\pi}{4}+cosx.sin\frac{\pi}{4}\right)=\sqrt{2}sin\left(x+\frac{\pi}{4}\right)\)
i/
\(sinx-cosx=\sqrt{2}\left(sinx.\frac{\sqrt{2}}{2}-cosx.\frac{\sqrt{2}}{2}\right)\)
\(=\sqrt{2}\left(sinx.cos\frac{\pi}{4}-cosx.sin\frac{\pi}{4}\right)=\sqrt{2}sin\left(x-\frac{\pi}{4}\right)\)
j/
\(cosx-sinx=\sqrt{2}\left(cosx.\frac{\sqrt{2}}{2}-sinx\frac{\sqrt{2}}{2}\right)\)
\(=\sqrt{2}\left(cosx.cos\frac{\pi}{4}-sinx.sin\frac{\pi}{4}\right)=\sqrt{2}cos\left(x+\frac{\pi}{4}\right)\)
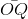 = cosα;
= cosα; 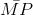 =
= 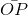 = sinα;
= sinα;
a) Để tìm góc a khi sin a = 1/2, ta sử dụng bảng giá trị của sin trong khoảng từ 0° đến 180°. Ta thấy rằng sin a = 1/2 tại góc 30° và góc 150°. Vậy, trong trường hợp này, có hai giá trị của góc a là 30° và 150°. b) Để tìm góc a khi cos a = 0, ta sử dụng bảng giá trị của cos trong khoảng từ 0° đến 180°. Ta thấy rằng cos a = 0 tại góc 90°. Vậy, trong trường hợp này, giá trị của góc a là 90°. c) Để tìm góc a khi tan a = -√3, ta sử dụng bảng giá trị của tan trong khoảng từ 0° đến 180°. Ta thấy rằng tan a = -√3 tại góc 120°. Vậy, trong trường hợp này, giá trị của góc a là 120°. Tóm lại, trong các trường hợp đã cho: a) sin a = 1/2: a = 30° và 150°. b) cos a = 0: a = 90°. c) tan a = -√3: a = 120°.