Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chắc là được sử dụng kiến thức 12 chứ?
\(\Leftrightarrow m\left(\sqrt{x^2+2}-1\right)\ge x\)
\(\Leftrightarrow m\ge\frac{x}{\sqrt{x^2+2}-1}\)
BPT có nghiệm khi và chỉ khi \(m\ge\min\limits_{x\in R}\frac{x}{\sqrt{x^2+2}-1}\)
Đặt \(f\left(x\right)=\frac{x}{\sqrt{x^2+2}-1}\Rightarrow f'\left(x\right)=\frac{2-\sqrt{x^2+2}}{\sqrt{x^2+2}\left(\sqrt{x^2+2}-1\right)^2}\)
\(f'\left(x\right)=0\Leftrightarrow\sqrt{x^2+2}=2\Leftrightarrow x=\pm\sqrt{2}\)
Từ BBT ta thấy hàm đạt cực tiểu tại \(x=-\sqrt{2}\)
\(\Rightarrow f\left(x\right)_{min}=f\left(-\sqrt{2}\right)=-\sqrt{2}\)
\(\Rightarrow m\ge-\sqrt{2}\)

Cho e hỏi là vì sao khúc cuối có dấu bằng mà trên đề k có dấu bằng ạ?
Vì mình lấy giá trị nguyên bạn
Chính xác là \(-\frac{1}{4}< k< \frac{2020-\frac{\pi}{2}}{2\pi}\)
\(\Rightarrow-0,25< k< 321,243\) (1)
Nhưng k nguyên nên chỉ cần lấy khoảng ở số nguyên gần nhất, tức là \(0\le k\le321\)

\(\Leftrightarrow\sqrt{2}sin\left(x+\frac{\pi}{4}\right)=\sqrt{2}\left(m^2+1\right)\)
\(\Leftrightarrow sin\left(x+\frac{\pi}{4}\right)=m^2+1\)
Do \(-1\le sin\left(x+\frac{\pi}{4}\right)\le1\) nên pt vô nghiệm khi và chỉ khi:
\(\left[{}\begin{matrix}m^2+1< -1\\m^2+1>1\end{matrix}\right.\) \(\Leftrightarrow m\ne0\)
Vậy \(m\ne0\)


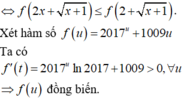
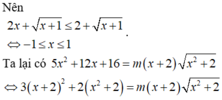
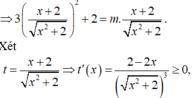
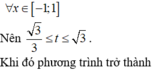
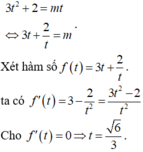
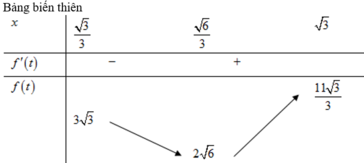
ĐKXĐ: \(x\le1\)
Bình phương 2 vế:
\(3-2x+2\sqrt{x^2-3x+2}=m+x-x^2\)
\(\Leftrightarrow x^2-3x+2+2\sqrt{x^2-3x+2}+1=m\)
\(\Leftrightarrow\left(\sqrt{x^2-3x+2}+1\right)^2=m\) (\(m\ge1\))
\(\Leftrightarrow\sqrt{x^2-3x+2}=\sqrt{m}-1\)
\(\Leftrightarrow x^2-3x+2=m+1-2\sqrt{m}\)
\(\Leftrightarrow x^2-3x=m-2\sqrt{m}-1\)
Xét parabol \(y=x^2-3x\) với \(x\le1\), do parabol chỉ có 1 nhánh nên \(y=m-2\sqrt{m}-1\) chỉ cắt parabol tại nhiều nhất 1 điểm????????
sai de ak