Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có |x-2006| \(\ge\) 0 với mọi x
(x-y+1)^2 \(\ge\)0 với mọi x;y
=>|x-2006|+(x-y+1)^2+2008 \(\ge\) 2008 với mọi x;y
Dấu "=" sảy ra khi x-2006=0 => x=2006
x-y+1=0 =>2006-y+1=0 => 2006-y=-1 => y=2006+1=2007
Vậy Min M=2008 tại x=2006 và y=2007

mk ko viết lại đề đâu nha làm luôn đấy
M=|3-x|+|x-7|+|x+2018|
\(\le\left|3-x+x+2018\right|+\)\(\left|x-7\right|\)
=|2021|+|x-7|
Dấu "=" xảy ra khi (3-x)(x+2018)\(\ge0\)
\(\Leftrightarrow\hept{\begin{cases}3-x\ge0\\x+2018\ge0\end{cases}}\Leftrightarrow\hept{\begin{cases}x\ge3\\x\le2018\end{cases}\Rightarrow3\le x\le2018}\)
Do |x-7|\(\ge0\) nên GTNN của M=2021 khi và chỉ khi x-7=0 => x=7(t/m \(3\le x\le2018\))
vậy GTNN của M=2021 khi x=7
tk cho mk nha bn
***** Chúc bạn học giỏi*****
Mik cũng làm được kết quả như bạn!! Hihi. Dù sao cũng cảm ơn bạn nhiều nha...

a)Ta có: \(x^2\ge0\Rightarrow x^2+3\ge3\)
Dấu "=" xảy ra \(\Leftrightarrow x=0\)
Vậy \(A_{Min}=3 khi x=0\)
b) \(\left(2x+1\right)^2\ge0\Rightarrow\left(2x+1\right)^2-5\ge-5\)
Dấu "=" xảy ra \(\Leftrightarrow x=-\dfrac{1}{2}\)
Vậy \(B_{Min}=-5khix=-\dfrac{1}{2}\)
c) \(\left(2x-1\right)^{2008}\ge0\)
Dấu "=" xảy ra \(\Leftrightarrow x=\dfrac{1}{2}\)
\(\left(3y-2\right)^{2008}\ge0\)
Dấu "=" xảy ra \(\Leftrightarrow y=\dfrac{2}{3}\)
\(\Rightarrow\left(2x-1\right)^{2008}+\left(3y-2\right)^{2008}\ge0\)
Dấu "=" xảy ra \(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{2}\\y=\dfrac{2}{3}\end{matrix}\right.\)
Vậy \(C_{Min}=0khix=\dfrac{1}{2}vày=\dfrac{2}{3}\)

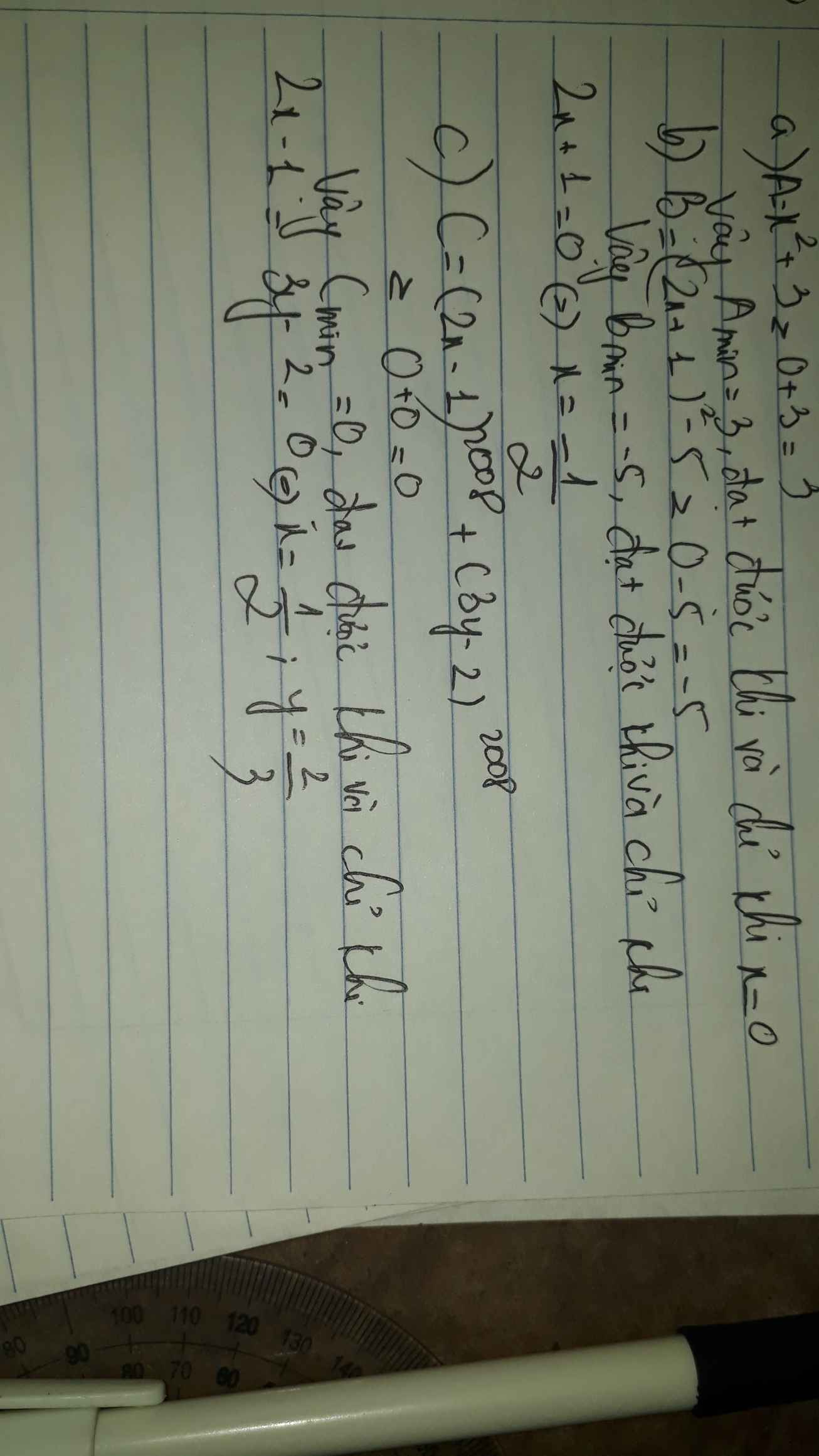
Cho mk sửa lại đề nha!
Tìm giá trị nhỏ nhất của biểu thức:
A = | x - 2008 | + | x - 1|