Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Với các bài toán tìm max, min 2 biến kiểu như thế này, em hay cố gắng nhân M lên n lần để tạo thêm được các số hạng, sang đó ghép tạo thành các bình phương.
Cách làm như sau:
\(4M=4a^2+4ab+4b^2-12a-12b+8004\)
\(=\left(4a^2+4ab+b^2\right)-6\left(2a+b\right)+3\left(b^2-2b\right)+8004\)
\(=\left(2a+b\right)^2-6\left(2a+b\right)+9+3\left(b^2-2b+1\right)+7992\)
\(=\left(2a+b-3\right)^2+3\left(b-1\right)^2+7992\ge7992\)
Vậy 4M min = 7992, vây M min = 1998.
Vậy min M = 1998 khi \(\hept{\begin{cases}b-1=0\\2a+b-3=0\end{cases}}\Rightarrow\hept{\begin{cases}b=1\\a=1\end{cases}}\)

GTNN = -10
cách làm
M = ...
= 2(a2+b2)+a2+b2+c2
= 2(a2+b2)+(a+b+c)2-2(ab+bc+ac) (1)
mà ab+bc+ac=5
=> (1) = 2(a2+b2)+(a+b+c)2-10
có a2 và b2 \(\ge\) 0
2 >0
(a+b+c)2 \(\ge\) 0
=> (1) \(\ge\) -10
=> M min = -10
hơi sơ sài nhỉ, ko hiểu thì hỏi, tôi chỉ cho

Tìm GTNH: P=x^2+xy+y^2-3x-3y+2010? - Yahoo Hỏi & Đáp
https://vn.answers.yahoo.com/question/index?qid=20100903224130AAhmqxW

cháu tôi học ghê thế :))
a) 3x3 - 7x2 + 17x - 5
= 3x3 - x2 - 6x2 + 2x + 15x - 5
= x2( 3x - 1 ) - 2x( 3x - 1 ) + 5( 3x - 1 )
= ( 3x - 1 )( x2 - 2x + 5 )
b) Đặt A = a2 + ab + b2 - 3a - 3b + 3
=> 4A = 4a2 + 4ab + 4b2 - 12a - 12b + 12
= ( 4a2 + 4ab + b2 - 12a - 6b + 9 ) + ( 3b2 - 6b + 3 )
= ( 2a + b - 3 )2 + 3( b - 1 )2 ≥ 0 ∀ a, b
hay 4A ≥ 0 => A ≥ 0
Dấu "=" xảy ra <=> a = b = 1
a.
\(3x^3-7x^2+17x-5=3x^3-x^2-6x^2+2x+15x-5\)
\(=\left(3x-1\right)\left[x^2-2x+5\right]\)
b.\(a^2+ab+b^2-3a-3b+3=\left(a-1\right)^2+\left(b-1\right)^2+\left(a-1\right)\left(b-1\right)\)
\(=\left[a-1+\frac{b-1}{2}\right]^2+\frac{3}{4}\left(b-1\right)^2\ge0\)
dấu bằng xảy ra khi \(a-1=b-1=0\Leftrightarrow a=b=1\)


a) A = x2 + 12x + 39
= ( x2 + 12x + 36 ) + 3
= ( x + 6 )2 + 3 ≥ 3 ∀ x
Đẳng thức xảy ra ⇔ x + 6 = 0 => x = -6
=> MinA = 3 ⇔ x = -6
B = 9x2 - 12x
= 9( x2 - 4/3x + 4/9 ) - 4
= 9( x - 2/3 )2 - 4 ≥ -4 ∀ x
Đẳng thức xảy ra ⇔ x - 2/3 = 0 => x = 2/3
=> MinB = -4 ⇔ x = 2/3
b) C = 4x - x2 + 1
= -( x2 - 4x + 4 ) + 5
= -( x - 2 )2 + 5 ≤ 5 ∀ x
Đẳng thức xảy ra ⇔ x - 2 = 0 => x = 2
=> MaxC = 5 ⇔ x = 2
D = -4x2 + 4x - 3
= -( 4x2 - 4x + 1 ) - 2
= -( 2x - 1 )2 - 2 ≤ -2 ∀ x
Đẳng thức xảy ra ⇔ 2x - 1 = 0 => x = 1/2
=> MaxD = -2 ⇔ x = 1/2
Ta có A = x2 + 12x + 39 = (x2 + 12x + 36) + 3 = (x + 6)2 + 3 \(\ge\)3
Dấu "=" xảy ra <=> x + 6 = 0
=> x = -6
Vậy Min A = 3 <=> x = -6
Ta có B = 9x2 - 12x = [(3x)2 - 12x + 4] - 4 =(3x - 2)2 - 4 \(\ge\)-4
Dấu "=" xảy ra <=> 3x - 2 =0
=> x = 2/3
Vậy Min B = -4 <=> x = 2/3
b) Ta có C = 4x - x2 + 1 = -(x2 - 4x - 1) = -(x2 - 4x + 4) + 5 = -(x - 2)2 + 5 \(\le\)5
Dấu "=" xảy ra <=> x - 2 = 0
=> x = 2
Vậy Max C = 5 <=> x = 2
Ta có D = -4x2 + 4x - 3 = -(4x2 - 4x + 1) - 2 = -(2x - 1)2 - 2 \(\le\)-2
Dấu "=" xảy ra <=> 2x - 1 = 0
=> x = 0,5
Vậy Max D = -2 <=> x = 0,5

a) A = x2 - 6x + 13 = x2 - 2.x.3 + 33 +4 = (x-3)2 + 4 >= 4 suy ra minA=4
mấy câu kia giải tương tự
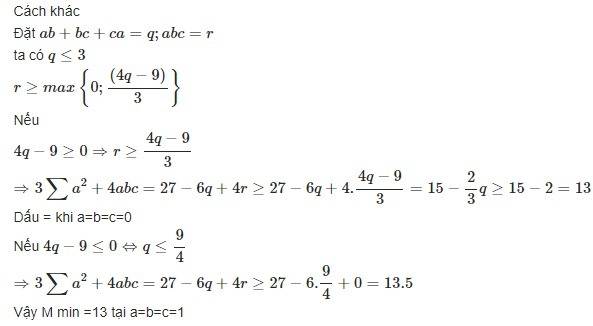
Lời giải:
Ta có:
\(4M=4a^2+4ab+4b^2-12a-12b+8052\)
\(=(4a^2+4ab+b^2)+3b^2-12a-12b+8052\)
\(=(2a+b)^2-6(2a+b)+9+3b^2-6b+8043\)
\(=[(2a+b)^2-6(2a+b)+9]+3(b^2-2b+1)+8040\)
\(=(2a+b-3)^2+3(b-1)^2+8040\)
\(\geq 0+3.0+8040=8040\)
\(\Rightarrow M\geq \frac{8040}{4}=2010\)
Vậy \(M_{\min}=2010\Leftrightarrow \left\{\begin{matrix} 2a+b-3=0\\ b-1=0\end{matrix}\right. \Rightarrow \left\{\begin{matrix} a=1\\ b=1\end{matrix}\right.\)