Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(P\left(x\right)=3x^2-\left[3f\left(x\right)+1\right]x+3-f\left(x\right)=0\left(1\right)\)
Phương trình (1) có nghiệm thuộc \(\left(0;\frac{2}{3}\right)\) khi:
\(\hept{\begin{cases}\Delta=9f^2\left(x\right)+18f\left(x\right)-35\ge0\\P\left(0\right)=3-f\left(x\right)>0\\P\left(\frac{2}{3}\right)=\frac{11}{3}-3f\left(x\right)>0\end{cases}\Leftrightarrow\hept{\begin{cases}f\left(x\right)\le\frac{-3-2\sqrt{11}}{3}\left(h\right)f\left(x\right)\ge\frac{-3+2\sqrt{11}}{3}\\f\left(x\right)< 3\\f\left(x\right)< \frac{11}{9}\end{cases}}}\)
\(\Rightarrow f\left(x\right)\in(-\infty;\frac{-3-2\sqrt{11}}{3}]\)U\([\frac{-3+2\sqrt{11}}{3};\frac{11}{9})\)
Dễ thấy \(f\left(x\right)>0\forall x\in\left(0;\frac{2}{3}\right)\). Suy ra \(\frac{-3+2\sqrt{11}}{3}\le f\left(x\right)< \frac{11}{9}\)
Vậy \(minf\left(x\right)=\frac{-3+2\sqrt{11}}{3}\), đạt được khi \(x=\frac{-1+\sqrt{11}}{3}.\)

Đặt \(A\left(3,4\right),B\left(x,y\right),N\left(0,y\right),M\left(x,0\right)\).
Khi đó \(f\left(x,y\right)=\sqrt{\left(x-3\right)^2+\left(y-4\right)^2}+\left|x\right|+\left|y\right|\)
\(=BA+BM+BN\)
\(\ge BA+BO\)
\(\ge AO\)(theo bđt tam giác)
Dấu \(=\)khi \(B\equiv O\)suy ra \(x=y=0\).
Vậy \(minf\left(x,y\right)=f\left(0,0\right)=5\).

Ta có: \(4xy\le\left(x+y\right)^2\le1\)
\(\Leftrightarrow xy\le\dfrac{1}{4}\)
\(A=\left(1+\dfrac{1}{x^2}\right)\left(1+\dfrac{1}{y^2}\right)\)
\(=\left(1+\dfrac{1}{4x^2}+\dfrac{1}{4x^2}+\dfrac{1}{4x^2}+\dfrac{1}{4x^2}\right)\left(1+\dfrac{1}{4y^2}+\dfrac{1}{4y^2}+\dfrac{1}{4y^2}+\dfrac{1}{4y^2}\right)\)
\(\ge5\sqrt[5]{\dfrac{1}{4^4x^8}}.5\sqrt[5]{\dfrac{1}{4^4y^8}}\)
\(=25\sqrt[5]{\dfrac{1}{4^8}.\dfrac{1}{\left(xy\right)^8}}\ge25\sqrt[5]{\dfrac{1}{4^8}.\dfrac{1}{\left(\dfrac{1}{4}\right)^8}}=25\)

a) Ta lập bảng xét dấu
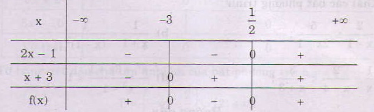
Kết luận: f(x) < 0 nếu - 3 < x <
f(x) = 0 nếu x = - 3 hoặc x =
f(x) > 0 nếu x < - 3 hoặc x > .
b) Làm tương tự câu a).
f(x) < 0 nếu x ∈ (- 3; - 2) ∪ (- 1; +∞)
f(x) = 0 với x = - 3, - 2, - 1
f(x) > 0 với x ∈ (-∞; - 3) ∪ (- 2; - 1).
c) Ta có: f(x) =
Làm tương tự câu b).
f(x) không xác định nếu x = hoặc x = 2
f(x) < 0 với x ∈ ∪
f(x) > 0 với x ∈ ∪ (2; +∞).
d) f(x) = 4x2 – 1 = (2x - 1)(2x + 1).
f(x) = 0 với x =
f(x) < 0 với x ∈
f(x) > 0 với x ∈ ∪

\(A=\left(2x+\dfrac{1}{3}\right)^4-1\ge-1\forall x\in R\)
Dấu "=" xảy ra khi\(2x+\dfrac{1}{3}=0\Leftrightarrow x=-\dfrac{1}{6}\)
\(B=-2\left(x-3\right)^2-\dfrac{7}{11}\left|3y+7\right|-2011\ge-2011\forall x,y\in R\)
Dấu "=" xảy ra khi \(\left\{{}\begin{matrix}x-3=0\\3y+7=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=-\dfrac{7}{3}\end{matrix}\right.\)
\(C=\left|2x+1\right|+\left|3-2x\right|\ge\left|2x+1+3-2x\right|=4\)
Dấu "=" xảy ra khi \(\left[{}\begin{matrix}2x+1=0\\3-2x=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{2}\\x=\dfrac{3}{2}\end{matrix}\right.\)

\(f\left(x\right)=4x+\frac{3}{\left(x+1\right)^2}=2x+2+2x+2+\frac{3}{\left(x+1\right)^2}-4\ge3\sqrt[3]{\left(2x+2\right)^2.\frac{3}{\left(x+1\right)^2}}-4\)
\(=3\sqrt[3]{48}-4\)
Dấu \(=\)khi \(2x+2=\frac{3}{\left(x+1\right)^2}\Leftrightarrow\left(x+1\right)^3=\frac{3}{2}\Leftrightarrow x=\sqrt[3]{\frac{3}{2}}-1\).

\(f\left(x\right)\ge\dfrac{\left(\sqrt{2}+2\right)^2}{x+2-x}-1=2+2\sqrt{2}\)
\(f\left(x\right)_{min}=2+2\sqrt{2}\) khi
\(x=2\sqrt{2}-2\)