
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Từ gt ta có x^2+y^^2=xy+1
=>P=(x^2+y^2)^2-2x^2y^2-x^2y^2
=(xy+1)2-2x2y2-x2y2
=x2y2+xy+1-3x2y2=-2x2y2+xy+1
=......
\(1=x^2+y^2-xy\ge2xy-xy=xy\Rightarrow xy\le1\)
\(1=x^2+y^2-xy\ge-2xy-xy=-3xy\Rightarrow xy\ge-\dfrac{1}{3}\)
\(\Rightarrow-\dfrac{1}{3}\le xy\le1\)
\(P=\left(x^2+y^2\right)^2-2\left(xy\right)^2-\left(xy\right)^2=\left(xy+1\right)^2-3\left(xy\right)^2=-2\left(xy\right)^2+2xy+1\)
Đặt \(xy=t\in\left[-\dfrac{1}{3};1\right]\)
\(P=f\left(t\right)=-2t^2+2t+1\)
\(f'\left(t\right)=-4t+2=0\Rightarrow t=\dfrac{1}{2}\)
\(f\left(-\dfrac{1}{3}\right)=\dfrac{1}{9}\) ; \(f\left(\dfrac{1}{2}\right)=\dfrac{3}{2}\) ; \(f\left(1\right)=1\)
\(\Rightarrow P_{max}=\dfrac{3}{2}\) ; \(P_{min}=\dfrac{1}{9}\)




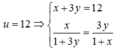
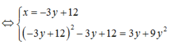
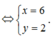
th1 : ta có : \(A=2017\left|x-2017\right|+\left|x-2018\right|\)
\(2017\left|x-2017\right|=A-\left|x-2018\right|\ge0\)
\(\Leftrightarrow A\ge\left|x-2018\right|\) dấu "=" xảy ra khi \(x=2017\) khi đó \(A=1\) (1)
th2 : ta có : \(A=2017\left|x-2017\right|+\left|x-2018\right|\)
\(\left|x-2018\right|=A-2017\left|x-2017\right|\ge0\)\(\Leftrightarrow A\ge2017\left|x-2017\right|\) dấu "=" xảy ra khi \(x=2018\) khi đó \(A=2017\) (2)
từ (1) và (2) ta có : giá trị nhỏ nhất của biểu thức \(A\) là \(1\) khi \(x=2017\)