Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
\(a,ĐK:x^2-1=\left(x-1\right)\left(x+1\right)\ne0\Leftrightarrow x\ne\pm1\\ \dfrac{3x+3}{x^2-1}=\dfrac{3\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}=\dfrac{3}{x-1}=2\\ \Leftrightarrow x-1=\dfrac{3}{2}\Leftrightarrow x=\dfrac{5}{2}\left(tm\right)\\ b,\dfrac{3}{x-1}\in Z\\ \Leftrightarrow x-1\inƯ\left(3\right)=\left\{-3;-1;1;3\right\}\\ \Leftrightarrow x\in\left\{-2;0;2;4\right\}\left(tm\right)\)
phân thức được xác định ⇔ x2 - 1 ≠ 0 ⇔ x ≠ \(\left\{-1;1\right\}\)
\(\dfrac{3x+3}{x^2-1}=-2\)
=> 3x + 3 = -2x2 + 2
=> 2x2 + 3x + 1 = 0
=> (2x+1)(x+1) = 0
=> x = -1/2 (thỏa mãn) hoặc x = -1 (loại)
Vậy, để phân thức có giá trị bằng –2 thì x = -1/2.
\(\dfrac{3x+3}{x^2-1}\)=\(\dfrac{3\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}\) (x khác -1 và x khác 1)
= \(\dfrac{3}{x-1}\)
=> Phân thức ban đầu có giá trị nguyên ⇔ 3 chia hết cho x-1
=> x-1 ∈\(\left\{-3;-1;1;3\right\}\)
=> x ∈\(\left\{-2;0;2;4\right\}\)
Vậy, để phân thức có giá trị là số nguyên.thì x ∈\(\left\{-2;0;2;4\right\}\).
a) ĐKXĐ: \(x\notin\left\{1;-1\right\}\)
b) Ta có: \(\dfrac{3x+3}{x^2-1}\)
\(=\dfrac{3\left(x+1\right)}{\left(x+1\right)\left(x-1\right)}\)
\(=\dfrac{3}{x-1}\)
Để phân thức có giá trị bằng -2 thì \(\dfrac{3}{x-1}=-2\)
\(\Leftrightarrow x-1=\dfrac{-3}{2}\)
hay \(x=-\dfrac{1}{2}\)
Vậy: Để phân thức có giá trị bằng -2 thì \(x=-\dfrac{1}{2}\)
c) Để phân thức có giá trị là số nguyên thì \(3⋮x-1\)
\(\Leftrightarrow x-1\inƯ\left(3\right)\)
\(\Leftrightarrow x-1\in\left\{1;-1;3;-3\right\}\)
\(\Leftrightarrow x\in\left\{2;0;4;-2\right\}\)
Kết hợp ĐKXĐ, ta được:
\(x\in\left\{2;0;4;-2\right\}\)
Vậy: Để phân thức có giá trị là số nguyên thì \(x\in\left\{2;0;4;-2\right\}\)
ĐKXĐ : x2-5x khác 0
<=>x.(x-5) khác 0
<=> x khác 0 và x khác 5
a)
\(\frac{x^2-10x+25}{x^2-5x}=0\Rightarrow x^2-10x+25=0\Leftrightarrow\left(x-5\right)^2=0\)
<=>x-5=0
<=>x=5
Mà x khác 5 nên không có x nào thỏa mãn phân thức bằng 0
b)\(\frac{x^2-10x+25}{x^2-5x}=\frac{5}{2}\Leftrightarrow\frac{\left(x-5\right)^2}{x.\left(x-5\right)}=\frac{5}{2}\Leftrightarrow\frac{x-5}{x}=\frac{5}{2}\Leftrightarrow\frac{2.\left(x-5\right)}{2x}=\frac{5x}{2x}\)
\(\Rightarrow2\left(x-5\right)=5x\Leftrightarrow2x-10=5x\Leftrightarrow-3x=10\Leftrightarrow x=-\frac{10}{3}\)
c) \(\frac{x^2-10x+25}{x^2-5x}=\frac{\left(x-5\right)^2}{x.\left(x-5\right)}=\frac{x-5}{x}=1-\frac{5}{x}\)
Để phân thức trên nguyên thì : 1-5/x là số nguyên
=>5/x là số nguyên
=>x thuộc Ư(5)={1;-1;5;-5}
Mà x khác 5 nên: x={1;-1;-5}
Vậy x={1;-1;-5}
=[3x(x2-16)+44(x2-16)+44.16+x-4+3]/(x-4)
=3x(x+4)+44(x+4)+1+(44.16+3)/(x-4)
để là giá trị nguyên thì 44.16+3=707 chia hết cho x-4
vậy x-4 phải là ước của 707
707=7.101 => x-4=7 hoặc x-4=101
=>x =11 hoăc x=105
10x^2 - 7x - 5 2x - 3 5x + 4 10x^2 - 15x - 8x - 5 8x - 12 7 -
Ta có \(M=\frac{10x^2-7x-5}{2x-3}=5x+4+\frac{7}{2x-3}\)
Để \(M=5x+4+\frac{7}{2x-3}\) là số nguyên <=> \(\frac{7}{2x-3}\)là số nguyên
\(\Rightarrow7⋮2x-3\) hay \(2x-3\inƯ\left(7\right)\)
\(\RightarrowƯ\left(7\right)=\) { - 7; - 1; 1; 7 }
Ta có : 2x - 3 = 7 <=> 2x = 10 => x = 5 (t/m)
2x - 3 = 1 <=> 2x = 4 => x = 2 (t/m)
2x - 3 = - 1 <=> 2x = 2 => x = 1 (t/m)
2x - 3 = - 7 <=> 2x = - 4 => x = - 2 (t/m)
Vậy với x \(\in\) { - 2; 1; 2; 5 } thì M là số nguyên
Bài 3 :
a) Phân thức xác định \(\Leftrightarrow x^2-1\ne0\Leftrightarrow\left(x-1\right)\left(x+1\right)\ne0\)
\(\Rightarrow\hept{\begin{cases}x-1\ne0\\x+1\ne0\end{cases}\Leftrightarrow\hept{\begin{cases}x\ne1\\x\ne-1\end{cases}}}\)
Ta có :
\(A=\frac{3x+3}{x^2-1}=\frac{3\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}=\frac{3}{x-1}\)
Để A có giá trị bằng -2 thì \(\frac{3}{x-1}=-2\)
\(\Leftrightarrow3=-2x+2\)
\(\Leftrightarrow-2x=1\)
\(\Leftrightarrow x=\frac{-1}{2}\)
b) Để A là số nguyên thì :
\(3⋮x-1\)
\(\Rightarrow x-1\inƯ\left(3\right)=\left\{1;3;-1;-3\right\}\)
\(\Rightarrow x\in\left\{2;4;0;-2\right\}\)( thỏa mãn ĐKXĐ )
Vậy...........
\(a,ĐKXĐ:x\ne\pm1\)
Ta có : \(\frac{3x+3}{x^2-1}=\frac{3\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}=\frac{3}{x-1}\)
\(\Rightarrow\frac{3x+3}{x^2-1}=-2\Leftrightarrow\frac{3}{x-1}=-2\)
\(\Leftrightarrow-2\left(x-1\right)=3\)
\(\Leftrightarrow-2x+2=3\)
\(\Leftrightarrow-2x=1\)
\(\Leftrightarrow x=\frac{-1}{2}\)
\(b,\) Để phân thức \(\frac{3x+3}{x^2-1}\) có giá trị nguyên thì \(\frac{3}{x-1}\) có giá trị nguyên
\(\Rightarrow3⋮x-1\)
\(\Rightarrow x-1\inƯ\left(3\right)=\left\{\pm1;\pm3\right\}\)
\(\Rightarrow x\in\left\{0;2;-2;4\right\}\)
Vậy \(x=-2;0;2;4\)
a) ĐKXĐ: \(x\notin\left\{1;-1\right\}\)
b) Ta có: \(\dfrac{4x-4}{2x^2-2}\)
\(=\dfrac{4\left(x-1\right)}{2\left(x-1\right)\left(x+1\right)}\)
\(=\dfrac{2}{x+1}\)
Để phân thức có giá trị bằng -2 thì \(\dfrac{2}{x+1}=-2\)
\(\Leftrightarrow x+1=-1\)
hay x=-2(thỏa ĐK)
Điều kiện xác định của phân thức: x ≠ 1/2
Để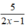
nguyên, 2x - 1 là ước của 5; Ta có
Ư
(
5
)
=
-
1
;
1
;
-
5
;
5
2x – 1 = -1 ⇒ 2x = 0 ⇒ x = 0 (thỏa mãn điều kiện xác định);
2x - 1 = 1 ⇒ 2x = 2 ⇒ x = 1 (thỏa mãn điều kiện xác định);
2x – 1 = -5 ⇒ 2x = -4 ⇒ x = -2 (thỏa mãn điều kiện xác định);
2x – 1 = 5 ⇒ 2x = 6 ⇒ x = 3 (thỏa mãn điều kiện xác định);
Vậy với x ∈ { -2; 0; 1; 3} thì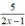
có giá trị nguyên.