H
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PL
4 tháng 8 2017
a)A=4-|2x+6|-|y+5|
Vì |2x+6| luôn lớn hơn hoặc bằng 0 với mọi x
|y+5| luôn lớn hơn hoặc bằng 0 với mọi y
=>|2x+6|-|y+5| luôn lớn hơn hoặc bằng 0 với mọi giá trị của x,y
=>4-|2x+6|-|y+5| luôn nhỏ hơn hoặc bằng 4
Vậy GTNN của biểu thức A là 4
Dấu bàng xảy ra khi |2x+6|=0 và |y+5|=0
Với |2x+6|=0 =>2x+6=0 =>2x=-6 =>x=-3
Với |y+5|=0 =>y+5=0 =>y=-5
Vậy Bieur thức A đạt GTNN là 4 khi x=-3;y=-5
b)B=12-|x-1|-|y+2|
Vì |x-1| luôn lớn hơn hoặc bằng 0 với moi x
|y+2| luôn lớn hơn hoặc bằng 0 với mọi y
=>|x-1|-|y+2| luôn nhỏ hơn hoặc bằng 0 với mọi giá trị của x,y
=>12-|x-1|-|y+2| luôn nhỏ hơn hoặc bằng 12
Vậy GTNN của biểu thức B là 12
Dấu bằng xảy ra khi |x-1|=0 và |y+2|=0
Với |x-1|=0 =>x-1=0 =>x=1
Với |y+2|=0 =>y+2=0 =>y=-2
Vậy biểu thức B đạt GTNN là 12 khi x=1 và y=-2
MA
28 tháng 8 2016
a) \(A=\left|x-\frac{2}{3}\right|-4\)
Có: \(\left|x-\frac{2}{3}\right|\ge0\)
\(\Rightarrow\left|x-\frac{2}{3}\right|-4\ge-4\)
Dấu '=' xảy ra khi: \(\left|x-\frac{2}{3}\right|=0\Rightarrow x=\frac{2}{3}\)
Vậy: \(Min_A=-4\) tại \(x=\frac{2}{3}\) ( K có GTLN bạn nhé )
b) \(B=2-\left|x+\frac{5}{6}\right|\) . Có: \(\left|x+\frac{5}{6}\right|\ge0\)
\(\Rightarrow2-\left|x+\frac{5}{6}\right|\le2\)
Dấu '=' xảy ra khi: \(\left|x+\frac{5}{6}\right|=0\Rightarrow x=-\frac{5}{6}\)
Vậy: \(Max_B=2\) tại \(x=-\frac{5}{6}\)
\(C=-\left|x+\frac{2}{3}\right|-4\). Có: \(-\left|x+\frac{2}{3}\right|\le0\)
\(\Rightarrow-\left|x+\frac{2}{3}\right|-4\le-4\)
Dấu '=' xảy ra khi: \(-\left|x+\frac{2}{3}\right|=0\Rightarrow x=-\frac{2}{3}\)
Vậy: \(Max_C=-4\) tại \(x=-\frac{2}{3}\)
T
28 tháng 11 2023
Giup mình với ah.
1- Tính :
A= 5. | x- 5 | - 3x + 1
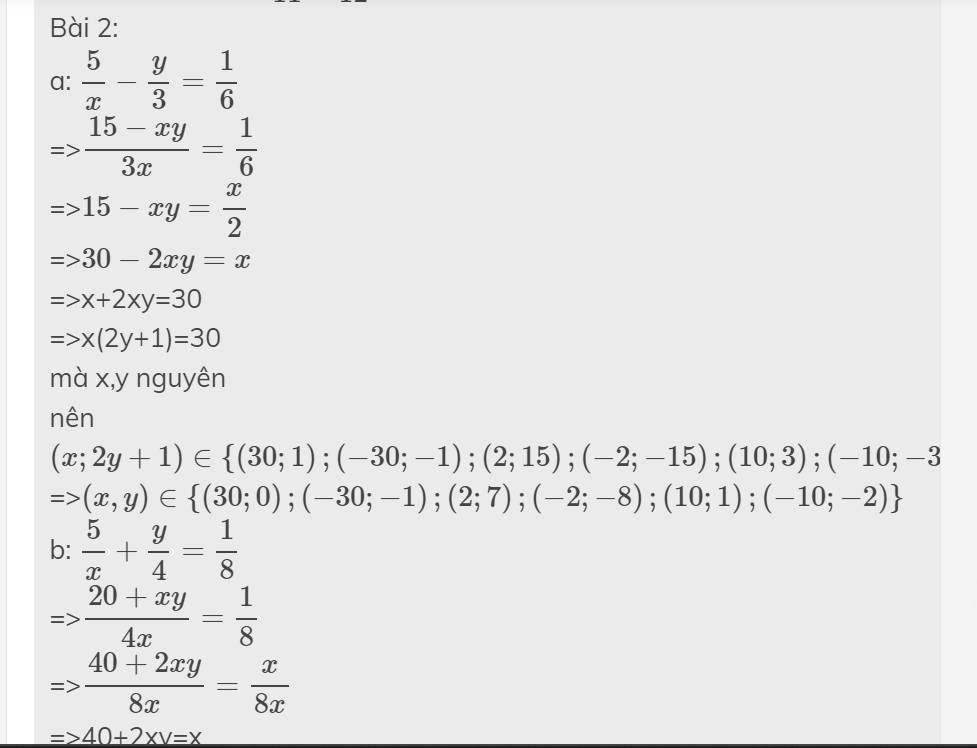
2 - Tìm các số nguyên x,y ; sao cho :
a) 5/x - y/3 = 1/6 b) 5/x + y/4 = 1/8
3- Tìm giá trị lớn nhất của Q = 27-2x/12-x ( x là số nguyên)
---------------------------------------------------------------------------------------------
8 tháng 9 2019
Hai bài này có mấy cái bình phương sẵn rồi nên chỉ sài cái bất đẳng thức \(A^2\ge0\)là được rồi
a/Ta có \(\left(2x+\frac{1}{3}\right)^4\ge0\)
Do đó \(\left(2x+\frac{1}{3}\right)^4-1\ge0-1\)
\(\Leftrightarrow A\ge-1\)
Tới đây vì A lớn hơn hoặc bằng -1 nên giá trị nhỏ nhất của A là -1
Vậy Giá trị nhỏ nhất của A là -1
b/Bạn làm hệt như câu a, với lại nếu bạn suy ra \(A\ge-1\)thì bạn kết luận luôn Giá trị nhỏ nhất của A là -1
VP
0
\(A=-\left(\frac{4}{9}x-\frac{12}{5}\right)^6+3\)
Có: \(-\left(\frac{4}{9}x-\frac{12}{5}\right)^6\le0\)
\(\Rightarrow A\le3\)
Dấu bằng xảy ra khi: \(-\left(\frac{4}{9}x-\frac{12}{5}\right)^6=0\Rightarrow\frac{4}{9}x-\frac{12}{5}=0\Rightarrow x=\frac{12}{5}.\frac{9}{4}=\frac{27}{5}\)
Vậy: \(Max_A=3;x=\frac{27}{5}\)
-(4/9.x-12/5)6 luôn luôn bé hơn hoặc bằng 0 do số mũ chẵn kết hợp với dấu âm
Ví dụ như -22= -4 bé hơn 0
Từ đó suy ra biểu thức A bé hơn hoặc bằng 3
Dấu bằng xảy ra khi 4/9x -12/5 =0 hay x =5.4 cũng là giá trị lớn nhất của A(=3)