
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có 64 = -8a + 4b - 2c + d; -61 = 27a + 9b + 3c +d
Từ y ' = 3 a x 2 + 2 b x + c ta thu được hai phương trình 0 = 12a - 4b + c; 0 = 27a + 6b + c
Giải hệ gồm 4 phương trình trên ta thu được a = 2; b = -3; c = -36; d = 20 hay a + b + c + d = -17
Đáp án C

\(M>\frac{x}{x+y+z+t}+\frac{y}{x+y+z+t}+\frac{z}{x+y+z+t}+\frac{t}{x+y+z+t}=\frac{x+y+z+t}{x+y+z+t}=1\)
Mà \(\frac{a}{b}<1\) thì \(\frac{a}{b}<\frac{a+m}{b+m}\) ; \(m\in N\)*
Do đó \(M<\frac{x+t}{x+y+z+t}+\frac{y+z}{x+y+z+t}+\frac{z+x}{x+y+z+t}+\frac{t+y}{x+y+z+t}=\frac{2\left(x+y+z+t\right)}{x+y+z+t}=2\)
Vậy 1 < M < 2 nên M không phải là số tự nhiên/

Chọn D.
Phương pháp: Sử dụng các tính chất hàm số đa thức bậc 3.

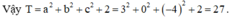

2) Ta có:
\(B=x^4+2x^3y-2x^3+x^2y^2-2x^2y-x\left(x+y\right)+2x+3\)
\(=x^4+x^3y-2x^3+x^3y+x^2y^2-2x^2y-x\left(x+y\right)+2x+3\)
\(=\left(x^4+x^3y-2x^3\right)+\left(x^3y+x^2y^2-2x^2y\right)-\left[x\left(x+y\right)-2x\right]+3\)
Do \(x+y-2=0\Rightarrow x+y=2\)
\(\Rightarrow B=\left(x^4+x^3y-2x^3\right)+\left(x^3y+x^2y^2-2x^2y\right)-\left[2x-2x\right]+3\)
\(=x^3.\left(x+y-2\right)+x^2y\left(x+y-2\right)-0+3\)
\(=0+0+3\)
\(=3\)
Vậy \(B=3\)
1) Ta có:
\(A=x^3+x^2y-2x^2-xy-y^2+3y+x-1\)
\(=\left(x^3+x^2y-2x^2\right)-\left(xy+y^2-2y\right)+y+x-1\)
\(=x^2\left(x+y-2\right)-y\left(x+y-2\right)+\left(x+y-2\right)+1\)
\(=0+0+0+1\)
\(=1\)
Vậy \(A=1\)

vì đồ thị hàm số đi qua điểm \(A\left(-1;\frac{5}{2}\right)\) nên tọa độ của A thỏa mãn phương trình sau: \(\frac{a+b}{-2}=\frac{5}{2}\Rightarrow a+b=-5\)(*)
ta tính y' có:
\(y'=\frac{\left(2ax-b\right)\left(x-1\right)-\left(ax^2-bx\right)}{\left(x-1\right)^2}=\frac{2ax^2-2ax-bx+b-ax^2+bx}{\left(x-1\right)^2}=\frac{ax^2-2ax+b}{\left(x-1\right)^2}\)
vì hệ số góc của tiếp tuyến tại điểm O(0;0) bằng 3 nên \(y'\left(O\right)=\frac{b}{\left(0-1\right)^2}=-3\Rightarrow b=-3\)
thay b=-3 vào (*) ta tìm được a=-2
vậy a=-2;b=-3

vì (C) đi qua điểm A nên tọa độ điểm A thỏa mãn pt \(y=\frac{ax^2-bx}{x-1}\) ta có \(\frac{5}{2}=\frac{a+b}{-2}\Rightarrow a+b=-5\)
vì tiếp tuyến của đồ thị tại điểm O có hệ số góc =-3 suy ra y'(O)=-3
ta có \(y'=\frac{ax^2-2ax+b}{\left(x-1\right)^2}\) ta có y'(O)=b=-3 suy ra a=-2
vậy ta tìm đc a và b

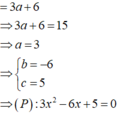
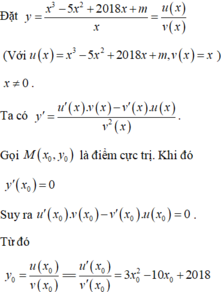

Chọn đáp án A
Phương pháp
Nhận thấy đây là hàm đa thức bậc ba nên ta thực hiện các bước sau:
+ Tìm y’, giải phương trình y’=0 ta tìm được nghiệm a.
+ Tìm y’’, nếu y’’(a)>0 thì a là điểm cực tiểu của hàm số từ đó tính giá trị cực tiểu y(a).