K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CA
4
TT
19 tháng 2 2020
Câu 1 :
a) ĐKXĐ : \(\hept{\begin{cases}x+1\ne0\\2x-6\ne0\end{cases}}\) \(\Leftrightarrow\hept{\begin{cases}x\ne-1\\x\ne3\end{cases}}\)
b) Để \(P=1\Leftrightarrow\frac{4x^2+4x}{\left(x+1\right)\left(2x-6\right)}=1\)
\(\Leftrightarrow\frac{4x^2+4x-\left(x+1\right)\left(2x-6\right)}{\left(x+1\right)\left(2x-6\right)}=0\)
\(\Rightarrow4x^2+4x-2x^2+4x+6=0\)
\(\Leftrightarrow2x^2+8x+6=0\)
\(\Leftrightarrow x^2+4x+4-1=0\)
\(\Leftrightarrow\left(x+2-1\right)\left(x+2+1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x+1=0\\x+3=0\end{cases}}\) \(\Leftrightarrow\orbr{\begin{cases}x=-1\left(KTMĐKXĐ\right)\\x=-3\left(TMĐKXĐ\right)\end{cases}}\)
Vậy : \(x=-3\) thì P = 1.
D
1
LL
31 tháng 8 2018
a) \(\frac{x+5}{x^2+5x-6}\)
ĐKXĐ: \(x^2+5x-6=x^2+6x-x-6\)
\(x\left(x+6\right)-\left(x+6\right)=\left(x-1\right)\left(x+6\right)\)
\(\Rightarrow x\ne1\) và \(x\ne-6\)
b) \(\frac{1-x}{3x^2-7x-6}\)
ĐKXĐ: \(3x^2-7x-6=3x^2-9x+2x-6=\left(x-3\right)\left(3x+2\right)\)
\(\Rightarrow x\ne3\) và \(x\ne\frac{-2}{3}\)
31 tháng 10 2021
a:TXĐ D=R\{2}
b: \(P=\dfrac{x^2}{x^3-8}+\dfrac{x}{x^2+2x+4}+\dfrac{1}{x-2}\)
\(=\dfrac{2x^2-2x+x^2+2x+4}{\left(x-2\right)\left(x^2+2x+4\right)}\)
\(=\dfrac{3x^2+4}{x^3-8}\)
LN
0
KT
10 tháng 1 2018
BÀI 1:
a) \(ĐKXĐ:\) \(x-3\)\(\ne\)\(0\)
\(\Leftrightarrow\)\(x\)\(\ne\)\(3\)
b) \(A=\frac{x^3-3x^2+4x-1}{x-3}\)
\(=\frac{\left(x^3-3x^2\right)+\left(4x-12\right)+11}{x-3}\)
\(=\frac{x^2\left(x-3\right)+4\left(x-3\right)+11}{x-3}\)
\(=x^2+4+\frac{11}{x-3}\)
Để \(A\)có giá trị nguyên thì \(\frac{11}{x-3}\)có giá trị nguyên
hay \(x-3\)\(\notinƯ\left(11\right)=\left\{\pm1;\pm11\right\}\)
Ta lập bảng sau
\(x-3\) \(-11\) \(-1\) \(1\) \(11\)
\(x\) \(-8\) \(2\) \(4\) \(14\)
Vậy....
T
1
VT
13 tháng 4 2019
Điều kiện: X khác -1
\(A=\left(\frac{4}{x+1}-1\right):\frac{9+x^2}{x^2+2x+1}\)
\(=>A=\left(\frac{4}{x+1}-\frac{x+1}{x+1}\right):\frac{9+x^2}{\left(x+1\right)^2}\)
\(=>A=\frac{4-x-1}{x+1}\cdot\frac{\left(x+1\right)^2}{9+x^2}\)
\(=>A=\frac{\left(3-x\right)\cdot\left(x+1\right)}{9+x^2}\)
TL
1
19 tháng 1 2022
\(1+\frac{1}{x+2}=\frac{12}{x^3+8}\Leftrightarrow1+\frac{1}{x+2}=\frac{12}{\left(x+2\right)\left(x^2-2x+4\right)}\)
đk : \(x\ne2\)
\(x^2-2x+4=x^2-2x+1+3=\left(x-1\right)^2+3\ge3\ne0\)( luôn đúng )
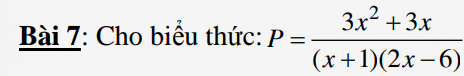
đk để xác định: \(x^2+1\ne0\)
=>x là số nào cũng được vì \(x^2+1\) luôn luôn > 0
A=1/(x^2+1)
A xác định khi x^2+1 khác 0
mà x^2+1 lớn hơn 0 với mọi x
suy ra A xác định với mọi GT của x