Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Điện áp ko đổi nhưng vẫn có dòng điện và dòng điện hữu hạn, chứng tỏ chỉ có 2 trường hợp:
1. Điện trở và cuộn cảm mắc nối tiếp (nối tiếp với tụ thì sẽ ko thể có dòng chạy qua)
2. Điện trở song song với tụ điện (nếu song song với cuộn cảm thuần thì sẽ bị chập mạch, tức là dòng lớn vô cùng)
Có thể bỏ qua trường hợp này vì điều kiện thứ 2.
Xét trường hợp 1:
Dễ dàng tính được: \(R=\frac{30}{2.5}=12\Omega\)
Mắc nối tiếp hộp kín với tụ điện C, ta có mạch RLC nối tiếp.
Theo bài ra, ta có hình vẽ: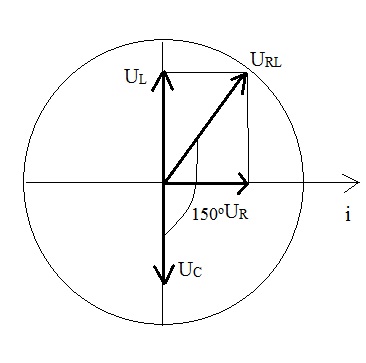
Từ hình vẽ ta có:
\(U_R=U_L\tan30^o\)
Suy ra:
\(Z_L=\frac{R}{\tan30^o}=12\sqrt{3}\Omega\)
Tổng trở của hộp kín:
\(Z=\sqrt{R^2+Z^2_L}=24\Omega\)

Khi C = C1 hoặc C = C2 thì I như nhau, do vậy:
\(Z_1=Z_2\Rightarrow Z_L-Z_{C1}=Z_{C2}-Z_L\Rightarrow Z_L=\dfrac{Z_{C1}+Z_{C2}}{2}=45\Omega\)
Để cường độ hiệu dụng qua R cực đại thì mạch xảy ra cộng hưởng.
\(\Rightarrow Z_C=Z_L=45\Omega\)
Chọn A.

Giải thích: Đáp án A
Phương pháp: Sử dụng hệ thức của định luật Ôm và công thức tính công suất tiêu thụ
Cách giải:
Giả sử cuộn dây thuần cảm:
Ta có, khi R = R2 công suất tiêu thụ trên biến trở cực đại.
Khi đó ta có: R2 = |ZL - ZC | = 40 - 25 = 15W
Mặt khác: 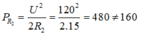
=> điều giả sử ban đầu là sai
=> Cuộn dây không thuần cảm có điện trở r
- Ta có:
+ Ban đầu khi mắc vào hai đầu A, M một ắc quy có suất điện động E = 12V, điện trở trong r1 = 4W thì I1 = 0,1875
Theo định luật Ôm, ta có: 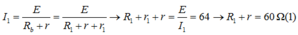
+ Khi mắc vào A,B một hiệu điện thế u = 120 2 cos(100πt), R = R2 thì công suất tiêu thụ trên biến trở cực đại và bằng 160W
Ta có:
Công suất trên biến trở R đạt cực đại khi ![]()
Mặt khác, ta có:
Công suất trên R2:
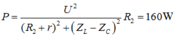
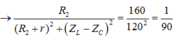
![]()
Kết hợp với (2) ta được: ![]()
Với r = 20W thay vào (1) => R1 = 60 - 20 = 40W
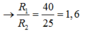

Bài này chỉ cần sử dụng công thức 2 giá trị của C để có cùng 1 giá trị của $U_C$ :
$U_C=U_{C_{max}} \cos \left(\dfrac{\varphi _1-\varphi _2}{2} \right)$
$\Rightarrow U_{C_{max}}=\dfrac{60}{\cos \dfrac{\pi }{6}}=40\sqrt{3} V$
Khi $U_{C_{max}}$ ta có:
$P=\dfrac{U^2}{R}\cos ^2\varphi _3=P_{max}\cos ^2\varphi _3=\dfrac{P_{max}}{2}$
$\Rightarrow \cos \varphi _3=\dfrac{\sqrt{2}}{2}$
Vẽ giản đồ suy ra: $U=\dfrac{U_{C_{max}}}{\sqrt{2}}=20\sqrt{6}\left(V \right)$

Giải thích: Đáp án A
Phương pháp: Cường độ dòng điện hiệu dụng I = U/Z
Đoạn mạch gồm RLC mắc nối tiếp : 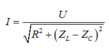 (1)
(1)
Khi nối tắt tụ : 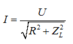
Từ (1) và (2)
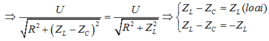
![]()
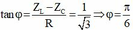
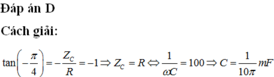
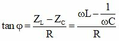

Ủa điện áp là hiệu điện thế đó :v
\(I=\dfrac{U}{R_1+R_2}=\dfrac{12}{2+10000}=...\left(A\right)\)
\(\Rightarrow U_1=I.R_1=2.I=...\left(V\right);U_2=12-U_1=...\left(V\right)\)