
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Hàm số tuần hoàn chu kỳ nên ta xét trên đoạn [− π ; π ].
y′ = − sinx – cosx
y′ = 0 ⇔ tanx = −1 ⇔ x = − π /4 + k π , k ∈ Z
Lập bảng biến thiên trên đoạn [− π ; π ]
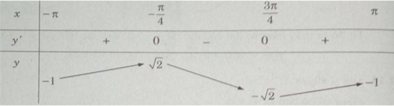
Hàm số đạt cực đại tại x = − π /4 + k2 π , đạt cực tiểu tại x = 3 π /4 + k2 π (k ∈ Z) và
y CD = y(− π /4 + k2 π ) = 2 ;
y CT = y(3 π /4 + k2 π ) = − 2 (k∈Z).

a) y = sin2x
Hàm số có chu kỳ T = π
Xét hàm số y=sin2x trên đoạn [0;π], ta có:
y' = 2cos2x
y' = 0 ⇔ 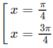
Bảng biến thiên:
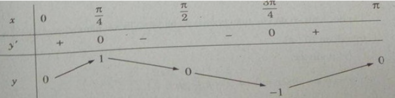
Do đó trên đoạn [0;π] , hàm số đạt cực đại tại π/4 , đạt cực tiểu tại 3π/4 và y C D = y(π/4) = 1; y C T = y(3π/4) = −1
Vậy trên R ta có:
y C Đ = y(π/4 + kπ) = 1;
y C T = y(3π/4 + kπ) = −1, k∈Z
b) Hàm số tuần hoàn chu kỳ nên ta xét trên đoạn [−π;π].
y′ = − sinx – cosx
y′ = 0 ⇔ tanx = −1 ⇔ x = −π4 + kπ, k∈Z
Lập bảng biến thiên trên đoạn [−π;π]
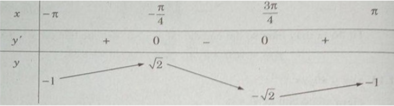
Hàm số đạt cực đại tại x = −π4 + k2π , đạt cực tiểu tại x = 3π4 + k2π (k∈Z) và
y C Đ = y(−π4 + k2π) = 2 ;
y C T = y(3π4 + k2π) = − 2 (k∈Z).
c) Ta có:
![]()
Do đó, hàm số đã cho tuần hoàn với chu kỳ π.
Ta xét hàm số y trên đoạn [0;π]:
![]()
y′ = sin2x
y′ = 0 ⇔ sin2x = 0 ⇔ x = kπ/2 (k∈Z)
Lập bảng biến thiên trên đoạn [0,π]
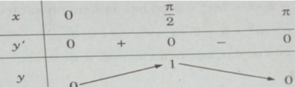
Từ đó, ta thấy hàm số đạt cực tiểu tại x = kπ/2 với k chẵn, đạt cực đại tại x = kπ/2 với k lẻ, và
y C T = y(2mπ) = 0; yCT = y(2mπ) = 0;
y C Đ = y((2m+1)π/2) = 1 (m∈Z)

TXĐ: D = R
+ y’ = cos x – sin x.
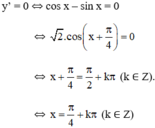
+ y’’ = -sin x – cos x = 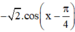
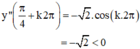
⇒ 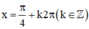 là các điểm cực đại của hàm số.
là các điểm cực đại của hàm số.
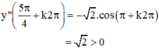
⇒ 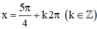 là các điểm cực tiểu của hàm số.
là các điểm cực tiểu của hàm số.

Xét tính chẵn lẻ:
a) TXĐ: D = R \ {π/2 + kπ| k nguyên}
Với mọi x thuộc D ta có (-x) thuộc D và
\(f\left(-x\right)=\frac{3\tan^3\left(-x\right)-5\sin\left(-x\right)}{2+\cos\left(-x\right)}=-\frac{3\tan^3x-5\sin x}{2+\cos x}=-f\left(x\right)\)
Vậy hàm đã cho là hàm lẻ
b) TXĐ: D = R \ \(\left\{\pm\sqrt{2};\pm1\right\}\)
Với mọi x thuộc D ta có (-x) thuộc D và
\(f\left(-x\right)=\frac{\sin\left(-x\right)}{\left(-x\right)^4-3\left(-x\right)^2+2}=-\frac{\sin x}{x^4-3x^2+2}=-f\left(x\right)\)
Vậy hàm đã cho là hàm lẻ
Tìm GTLN, GTNN:
TXĐ: D = R
a) Ta có (\(\left(\sin x+\cos x\right)^2=1+\sin2x\)
Với mọi x thuộc D ta có\(-1\le\sin2x\le1\Leftrightarrow0\le1+\sin2x\le2\Leftrightarrow0\le\left(\sin x+\cos x\right)^2\le2\)
\(\Leftrightarrow0\le\left|\sin x+\cos x\right|\le\sqrt{2}\Leftrightarrow-\sqrt{2}\le\sin x+\cos x\le\sqrt{2}\)
Vậy \(Min_{f\left(x\right)}=-\sqrt{2}\) khi \(\sin2x=-1\Leftrightarrow2x=-\frac{\pi}{2}+k2\pi\Leftrightarrow x=-\frac{\pi}{4}+k\pi\)
\(Max_{f\left(x\right)}=\sqrt{2}\) khi\(\sin2x=1\Leftrightarrow x=\frac{\pi}{4}+k\pi\)
b) Với mọi x thuộc D ta có:
\(-1\le\cos x\le1\Leftrightarrow-2\le2\cos x\le2\Leftrightarrow1\le2\cos x+3\le5\)
\(\Leftrightarrow1\le\sqrt{2\cos x+3}\le\sqrt{5}\Leftrightarrow5\le\sqrt{2\cos x+3}+4\le\sqrt{5}+4\)
Vậy\(Min_{f\left(x\right)}=5\) khi \(\cos x=-1\Leftrightarrow x=\pi+k2\pi\)
\(Max_{f\left(x\right)}=\sqrt{5}+4\) khi \(\cos x=1\Leftrightarrow x=k2\pi\)
c) \(y=\sin^4x+\cos^4x=\left(\sin^2x+\cos^2x\right)^2-2\sin^2x\cos^2x\)\(=1-\frac{1}{2}\left(2\sin x\cos x\right)^2=1-\frac{1}{2}\sin^22x\)
Với mọi x thuộc D ta có: \(0\le\sin^22x\le1\Leftrightarrow-\frac{1}{2}\le-\frac{1}{2}\sin^22x\le0\Leftrightarrow\frac{1}{2}\le1-\frac{1}{2}\sin^22x\le1\)
Đến đây bạn tự xét dấu '=' xảy ra khi nào nha :p

\(y'=cosx-sinx=0\)
\(\Leftrightarrow x=\frac{\pi}{4}+k\pi\)
\(y''=-sinx-cosx\)
\(y''\left(\frac{\pi}{4}+k2\pi\right)=-\sqrt{2}< 0\)
\(y''\left(\frac{\pi}{4}+\left(2k+1\right)\pi\right)=\sqrt{2}>0\)
\(\Rightarrow\) Hàm đạt cực đạt tại những điểm thỏa mãn \(x=\frac{\pi}{4}+k2\pi\)
Hàm đạt cực tiểu tại những điểm \(x=\frac{5\pi}{4}+k2\pi\)

ta tính \(y'=cosx+sinx=\sqrt{2}cos\left(x-\frac{\Pi}{4}\right)\)
giải pt y'=0 ta có
\(\sqrt{2}cos\left(x-\frac{\Pi}{4}\right)=0\Rightarrow x-\frac{\Pi}{4}=\frac{\Pi}{2}+k\Pi\Rightarrow x=\frac{3\Pi}{4}+k\Pi\)
ta tình \(y''=-sinx+cosx\)
ta có \(y''\left(\frac{-\Pi}{4}\right)=\sqrt{2}>0\)hàm số đạt cực tiểu tại x\(\frac{-\Pi}{4}+2k\Pi\)
ta có \(y''\left(\frac{3\Pi}{4}\right)=-\sqrt{2}<0\)hàm số đạt cực đại tại x=\(\frac{3\Pi}{4}+2k\Pi\)