PT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PT
1
CM
30 tháng 10 2019
TXĐ: R
y′ = 2(x + 2). x - 3 3 + 3 x + 2 2 . x - 3 2 = 5x(x + 2). x - 3 2
y′= 0 ⇔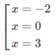 
Bảng biến thiên:
Từ đó suy ra y CĐ = y(-2) = 0; y CT = y(0) = -108.
PT
1
CM
27 tháng 4 2019
Hàm số xác định trên khoảng (− ∞ ;+ ∞ ).
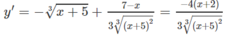
Bảng biến thiên:
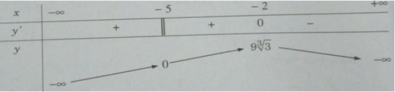
Vậy
y
CD
= y(−2) =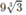 
PT
1
PT
1
CM
20 tháng 9 2019
TXĐ : R
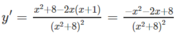
y′= 0 ⇔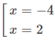 
Bảng biến thiên:
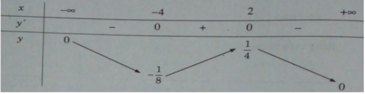
Hàm số đạt cực đại tại x = 2, cực tiểu tại x = -4 và y CD = y(2) = 1/4; y CT = y(−4) = −1/8
PT
1
CM
9 tháng 11 2017
TXĐ: R
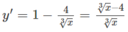
y′ = 0 ⇔ x = 64
Bảng biến thiên:
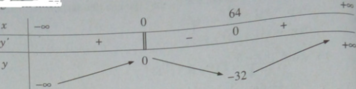
Vậy ta có y CD = y(0) = 0 và y CT = y(64) = -32.
CM
25 tháng 7 2018
TXĐ: D = R
+ y' = 2cos2x – 1;
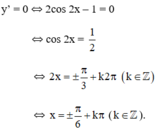
+ y" = -4.sin2x
⇒ 
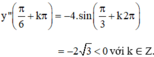
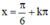(k ∈ Z) là các điểm cực đại của hàm số.
⇒ 
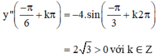
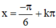(k ∈ Z) là các điểm cực tiểu của hàm số.
PT
1
CM
21 tháng 3 2019
TXĐ: R\{-1}
Hàm số đồng biến trên các khoảng và do đó không có cực trị.
CM
22 tháng 11 2017
Vì x 2 – 2x + 5 luôn luôn dương nên hàm số xác định trên (− ∞ ; + ∞ )
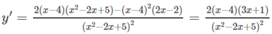
y′ = 0 ⇔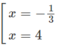 
Bảng biến thiên:
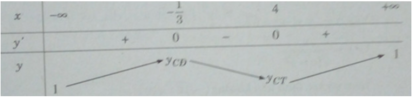
Hàm số đạt cực đại tại x = −1/3, đạt cực tiểu tại x = 4 và y CD = y(−1/3) = 13/4; y CT = y(4) = 0
Hàm số xác định trên khoảng (− 10 ; 10 ).
Vì y’ > 0 với mọi (− 10 ; 10 ) nên hàm số đồng biến trên khoảng đó và do đó không có cực trị.