PT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TM
5
21 tháng 11 2017
nh 98): Xét ΔABC và ΔABD có:
Nên ΔABC = ΔABD (g.c.g)
- Hình 99): Ta có:
Xét ΔABD và ΔACE có:
Nên ΔABD = ΔACE ( g.c.g)
Xét ΔADC và ΔAEB có:
DC = EB (Vì DC = DB + BC ; EB = EC + BC mà DB = EC)
Nên ΔADC = ΔAEB (g.c.g)
TH
21 tháng 11 2017
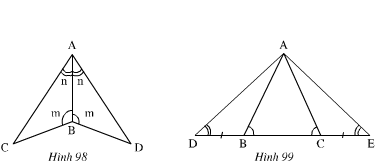
Xem hình 98)
∆ABC và ∆ABD có:
ˆA1A1^=ˆA2A2^(gt)
AB là cạnh chung.
ˆB1B1^=ˆB2B2^(gt)
Nên ∆ABC=∆ABD(g.c.g)
Xem hình 99)
Ta có:
ˆB1B1^+ˆB2B2^=1800 (Hai góc kề bù).
ˆC1C1^+ ˆC2C2^=1800 (Hai góc kề bù)
Mà ˆB2B2^=ˆC2C2^(gt)
Nên ˆB1B1^=ˆC1C1^
* ∆ABD và ∆ACE có:
ˆB1B1^=ˆC1C1^(cmt)
BD=EC(gt)
ˆDD^ = ˆEE^(gt)
Nên ∆ABD=∆ACE(g.c.g)
* ∆ADC và ∆AEB có:
ˆDD^=ˆEE^(gt)
ˆC2C2^=ˆB2B2^(gt)
DC=EB
Nên ∆ADC=∆AEB(g.c.g)
21 tháng 9 2017
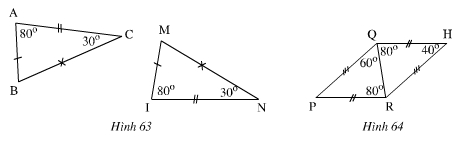
Hình 63
Ta có:
Và AB = MI; AC = IN; BC = MN
Nên ΔABC = ΔIMN
Hình 64 :
ΔPQR có:
Và QH = RP, HR = PQ, QR ( cạnh chung )
Nên ΔHQR = ΔPRQ
SK
2
RD
3
16 tháng 4 2018
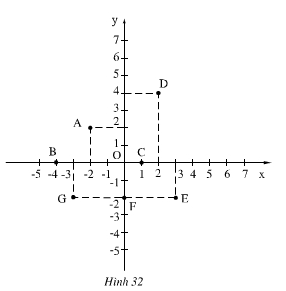
Tọa độ các điểm đó là:
A(-2; 2) ; B(-4; 0)
C(1; 0) ; D(2; 4)
E(3; -2) ; F(0; -2)
G(-3; -2)
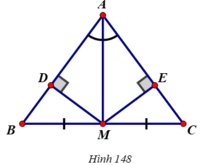
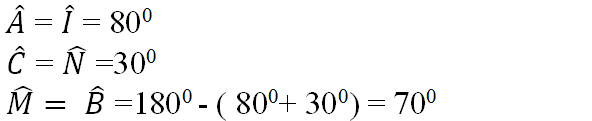
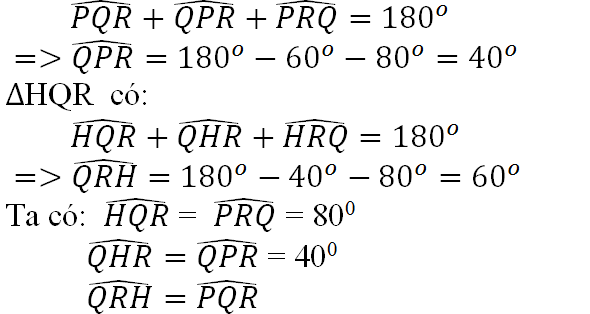
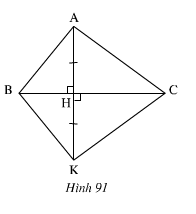
+ Hai tam giác vuông AMD và AME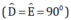
có:
AM chung
⇒ ΔAMD = ΔAME ( cạnh huyền - góc nhọn)
⇒ MD = ME và AD = AE ( Hai cạnh tương ứng) (1)
+ Hai tam giác vuông MDB và MEC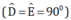
có
MB = MC (GT)
MD = ME (chứng minh trên)
⇒ ΔMDB = ΔMEC ( cạnh huyền – cạnh góc vuông)
⇒ BD=CE ( hai cạnh tương ứng) (2)
Từ (1) và (2) ⇒ AD+BD=AE+CE ⇒ AB=AC.
+ Xét ΔAMB và ΔAMC có:
MB = MC (GT)
AB = AC (chứng minh trên)
AM chung
⇒ ΔAMB = ΔAMC (c.c.c)