
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Giải:
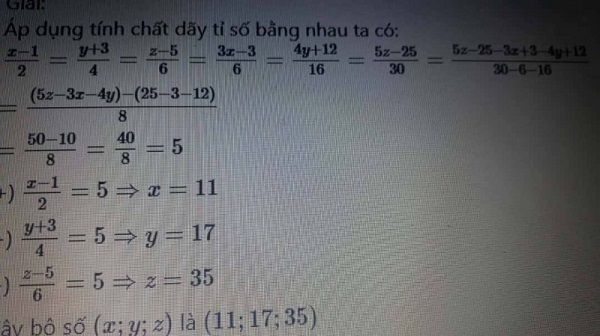
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
x−12=y+34=z−56=3x−36=4y+1216=5z−2530
=5z−25−3x+3−4y+1230−6−16
=(5z−3x−4y)−(25−3−12)8x−12=y+34=z−56=3x−36=4y+1216=5z−2530=5z−25−3x+3−4y+1230−6−16=(5z−3x−4y)−(25−3−12)8
=50−108=408=5=50−108=408=5
+) x−12=5⇒x=11x−12=5⇒x=11
+) y+34=5⇒y=17y+34=5⇒y=17
+) z−56=5⇒z=35z−56=5⇒z=35
Vậy bộ số (x;y;z)(x;y;z) l
à (11;17;35)
Ta có : \(\frac{x-1}{2}=\frac{y+3}{4}=\frac{z-5}{6}\Rightarrow\frac{-3x+3}{-6}=\frac{-4y-12}{-16}=\frac{5z-25}{30}\)
Theo tính chất dãy tỉ số bằng nhau
\(\frac{-3x+3}{-6}=\frac{-4y-12}{-16}=\frac{5z-25}{30}=\frac{-3x-4y+5z+3-12-25}{8}=2\)
\(\Rightarrow-3x+3=-12\Leftrightarrow-3x=-15\Leftrightarrow x=5\)
\(\Rightarrow-4y-12=-32\Leftrightarrow-4y=-20\Leftrightarrow y=5\)
\(\Rightarrow5z-25=60\Leftrightarrow z=17\)

Lời giải:
Đặt $\frac{x-1}{2}=\frac{y+3}{4}=\frac{z-5}{6}=a$
$\Rightarrow x=2a+1; y=4a-3; z=6a+5$
Thay vào điều kiện $5z-3x-4y=50$ thì:
$5(6a+5)-3(2a+1)-4(4a-3)=50$
$\Rightarrow 8a-16=0$
$\Rightarrow a=2$
Do đó:
$x=2a+1=2.2+1=5$
$y=4a-3=4.2-3=5$
$z=6a+5=6.2+5=17$

Ta có: x-1/2 = y+3/4 = z-5/6 = K
x = 2K+1 ; y = 4K+3 ; z = 6K+5
Thay các giá trị: x = 2K+1 ; y = 4K-3 ; z = 6K+5 vào biểu thức
5z - 3x - 4y = 50. Ta có,
5.(6K+5) - 3.(4K+3) - 4.(4K-3) = 50
<=> 30K + 25 - 6K - 3 - 16K + 12 = 50
<=> 8K + 34 = 50
<=> 8K = 50-34 = 16
<=> K = 16/8 = 2
=> x-1/2 = 2 => x-1 = 2.2 <=> x-1=4 => x=4+1=5
=>y-3/4 = 2 => y+3 = 2.4 <=> y+3 = 8 => y = 8-3=5
=> z-5/6 = 2 => z-5 = 2.6 <=> z-5 = 12 => z = 12+5=17


1, ta co \(\frac{x}{5}=\frac{y}{6}=\frac{x}{20}=\frac{y}{24}\)
\(\frac{y}{8}=\frac{z}{7}=\frac{y}{24}=\frac{z}{21}\)
=>\(\frac{x}{20}=\frac{y}{24}=\frac{z}{21}=\frac{x+y-z}{20+24-21}=\frac{69}{23}=3\)
=>\(x=3\cdot20=60\)
\(y=3\cdot24=72\)
\(z=3\cdot21=63\)
3. ta co \(\frac{x}{15}=\frac{y}{7}=\frac{z}{3}=\frac{t}{1}=\frac{x+y-z+t}{15-7+3-1}=\frac{10}{10}=1\)
=> \(x=1\cdot15=15\)
\(y=1\cdot7=7\)
\(z=1\cdot3=3\)
\(t=1\cdot1=1\)

Theo đề bài ta có : x−12=y+34=z−56x−12=y+34=z−56 và 5z−3x−4y=505z−3x−4y=50
\Leftrightarrow 3(x−1)6=4(y+3)16=5(z−5)303(x−1)6=4(y+3)16=5(z−5)30 và 5z−3x−4y=505z−3x−4y=50
\Leftrightarrow 3x−36=4y+1216=5z−25303x−36=4y+1216=5z−2530 và 5z−3x−4y=505z−3x−4y=50
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
3x−36=4y+1216=5z−2530=(5z−25)−(3x−3)−(4y+12)30−6−16=5z−3x−4y−25+3−128=168=23x−36=4y+1216=5z−2530=(5z−25)−(3x−3)−(4y+12)30−6−16=5z−3x−4y−25+3−128=168=2
\Rightarrow x−12=2x−12=2 \Rightarrow x−1=4x−1=4 \Leftrightarrow x=5x=5
\Rightarrow y+34=2y+34=2 \Rightarrow y+3=8y+3=8 \Leftrightarrow y=5y=5
\Rightarrow z−56=2z−56=2 \Rightarrow z−5=12z−5=12 \Leftrightarrow z=17
\(\dfrac{x+1}{2}=\dfrac{y+3}{4}=\dfrac{z-5}{6}\)
\(=\dfrac{3x+3}{6}=\dfrac{4y+12}{16}+\dfrac{5z-25}{30}\)
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(\dfrac{x+1}{2}=\dfrac{y+3}{4}=\dfrac{z-5}{6}=\dfrac{3x+3}{6}=\dfrac{4y+12}{16}+\dfrac{5z-25}{30}=\dfrac{5x-25-3x-3-4y-12}{30-16-6}=\dfrac{50-40}{8}=\dfrac{10}{8}=\dfrac{5}{4}\)
\(\Rightarrow\dfrac{x+1}{2}=\dfrac{5}{4}\Rightarrow x+1=2,5\)
\(\Rightarrow x=1,5.\)
\(\Rightarrow\dfrac{y+3}{4}=\dfrac{5}{4}\Rightarrow y+3=5\)
\(\Rightarrow y=2\)
\(\Rightarrow\dfrac{z-5}{6}=\dfrac{5}{4}\Rightarrow z-5=7,5\)
\(\Rightarrow z=12,5.\)
Vậy các số \(\left(x;y;z\right)\) cần tìm lần lượt là \(\left(1,5;2;12,5\right)\)