Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


(x+1)+(x+3)+...+(x+99)=0
Tổng các số hạng là: (99+1):2=50 (số hạng)
=> (x+1)+(x+3)+...+(x+99)=0 <=> 50.x+(1+3+5+...+99) = 0
<=> 50.x+\frac{\left(99+1\right).50}{2}2(99+1).50=0 <=> 50.x+2500=0 => x=-2500/50=-50

\(x\) + y = 2; ⇒ y = 2 - \(x\);
y + z = 3 ⇒ y = 3 - z
⇒ 2 - \(x\) = 3 - z ⇒ \(x\) = 2 - 3 + z ⇒ \(x\) = -1 + z
Thay \(x\) = -1 + z vào biểu thức z + \(x\) = -5 ta có:
z - 1 + z = -5
2z = -5 + 1 ⇒ 2z = -4 ⇒ z = -4: 2 ⇒ z = -2
Thay z = -2 vào biểu thức \(x\) = -1 + z ta có \(x\) = -1 -2 = -3
Thay z = -2 vào biểu thức y = 3 - z ta có: y = 3 - (-2) = 5

Ta có:
\(x\) và \(x^5\) có cùng tính chẵn - lẻ (cùng tính chẵn - lẻ nghĩa là nếu \(x\) lẻ thì \(x^5\) lẻ, còn nếu \(x\) chẵn thì \(x^5\) cũng chẵn luôn)
\(y\) và \(y^3\) có cùng tính chẵn - lẻ
\(\left(x+y\right)\) và \(\left(x+y\right)^2\) có cùng tính chẵn - lẻ
Vậy \(x^5+y^3-\left(x+y\right)^2\) và \(x+y-\left(x+y\right)\) có cùng tính chẵn - lẻ
Trong mọi trường hợp, dù \(x\) và \(y\) lẻ hay chẵn thì kết quả luôn là số chẵn\(\Rightarrow3z^3\) là số chẵn\(\Rightarrow z\) phải là số chẵn mà 2 là số nguyên tố chẵn duy nhất\(\Rightarrow z=2\)
\(\Rightarrow x^5+y^3-\left(x+y\right)^2=3\cdot2^3=24\)
Chỉ khi \(x=y=2\) thì phương trình trên mới hợp lí.
Vậy \(x=y=2\)
Đáp số: \(x=y=z=2\)

Bài toán không có lời giải vì không có số nguyên tố âm nên không có kết quả cho bài toán này

Bài 1
a) (x + 3)(x + 2) = 0
x + 3 = 0 hoặc x + 2 = 0
*) x + 3 = 0
x = 0 - 3
x = -3 (nhận)
*) x + 2 = 0
x = 0 - 2
x = -2 (nhận)
Vậy x = -3; x = -2
b) (7 - x)³ = -8
(7 - x)³ = (-2)³
7 - x = -2
x = 7 + 2
x = 9 (nhận)
Vậy x = 9
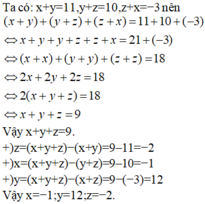
\(\Rightarrow x+y+y+z+z+x=11+3+2\\ \Rightarrow2\left(x+y+z\right)=16\\ \Rightarrow x+y+z=8\)
\(x+y+z-x-y=8-11\\ \Rightarrow z=-3\)
\(x+y+z-y-z=8-3\\ \Rightarrow x=5\)
\(x+y+z-z-x=8-2\\ \Rightarrow y=6\)