Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: \(=\dfrac{1-2x+3+2y+2y-4}{6x^3y}=\dfrac{-2x+4y}{6x^3y}=\dfrac{-2\left(x-2y\right)}{6x^3y}=\dfrac{-x+2y}{3x^3y}\)
b: \(=\dfrac{x^2-2+2-x}{x\left(x-1\right)^2}=\dfrac{x\left(x-1\right)}{x\left(x-1\right)^2}=\dfrac{1}{x-1}\)
c: \(=\dfrac{3x+1+x^6-3x}{x^2-3x+1}\)
\(=\dfrac{x^6+1}{x^2-3x+1}\)
d: \(=\dfrac{x^2+38x+4+3x^2-4x-2}{2x^2+17x+1}\)
\(=\dfrac{4x^2+34x+2}{2x^2+17x+1}=2\)

\(\frac{17x+18}{3x^2+x-14}=\frac{a}{x-2}+\frac{b}{3x+7}\)
\(\Rightarrow\frac{17x+18}{3x^2+x-14}=\frac{a\left(3x+7\right)+b\left(x-2\right)}{\left(x-2\right)\left(3x+7\right)}\)
\(\Rightarrow\frac{17x+18}{3x^2+x-14}=\frac{3ax+7a+bx-2b}{3x^2+x-14}\)
\(\Rightarrow\frac{17x+18}{3x^2+x-14}=\frac{3ax+5a+bx}{3x^2+x-14}\)
\(\Rightarrow\frac{17x+18}{3x^2+x-14}=\frac{\left(3a+b\right)x+5a}{3x^2+x-14}\)
Đồng nhất hệ số, ta có: \(\hept{\begin{cases}3a+b=17\\5a=18\end{cases}}\Leftrightarrow\hept{\begin{cases}b=\frac{31}{5}\\a=\frac{18}{5}\end{cases}}\)

áp dụng phương pháp trị số riêng ta có
\(\dfrac{a}{x-2}+\dfrac{b}{\left(x+1\right)^2}=\dfrac{a\left(x+1\right)^2+b\left(x-2\right)}{\left(x-2\right)\left(x+1\right)^2}\)
đồng nhất phân thức \(\dfrac{x^2+5}{x^3-3x-2},\)ta có với mọi x:
\(a\left(x+1\right)^2+b\left(x-2\right)=x^2+5\)\(\left(1\right)\)
vì \(\left(1\right)\)đúng với mọi x nên để xác định a và b ở \(\left(1\right)\)ta có thể cho x=-1,x=2
với x=-1 thì -3b=6 => b=-2
với x=2 thì 9a=9 => a =1

a) \(\dfrac{7}{8x^2-18}+\dfrac{1}{2x^2+3x}-\dfrac{1}{4x-6}\)
\(=\dfrac{7}{2\left(4x^2-9\right)}+\dfrac{1}{x\left(2x+3\right)}-\dfrac{1}{2\left(2x-3\right)}\)
\(=\dfrac{7}{2\left(2x-3\right)\left(2x+3\right)}+\dfrac{1}{x\left(2x+3\right)}-\dfrac{1}{2\left(2x-3\right)}\) MTC: \(2x\left(2x-3\right)\left(2x+3\right)\)
\(=\dfrac{7x}{2x\left(2x-3\right)\left(2x+3\right)}+\dfrac{2\left(2x-3\right)}{2x\left(2x-3\right)\left(2x+3\right)}-\dfrac{x\left(2x+3\right)}{2x\left(2x-3\right)\left(2x+3\right)}\)
\(=\dfrac{7x+2\left(2x-3\right)-x\left(2x+3\right)}{2x\left(2x-3\right)\left(2x+3\right)}\)
\(=\dfrac{7x+\left(4x-6\right)-\left(2x^2+3x\right)}{2x\left(2x-3\right)\left(2x+3\right)}\)
\(=\dfrac{7x+4x-6-2x^2-3x}{2x\left(2x-3\right)\left(2x+3\right)}\)
\(=\dfrac{-2x^2+8x-6}{2x\left(2x-3\right)\left(2x+3\right)}\)
\(=\dfrac{-2\left(x^2-4x+3\right)}{2x\left(2x-3\right)\left(2x+3\right)}\)
\(=\dfrac{-2\left(x^2-x-3x+3\right)}{2x\left(2x-3\right)\left(2x+3\right)}\)
\(=\dfrac{-2\left[\left(x^2-x\right)-\left(3x-3\right)\right]}{2x\left(2x-3\right)\left(2x+3\right)}\)
\(=\dfrac{-2\left[x\left(x-1\right)-3\left(x-1\right)\right]}{2x\left(2x-3\right)\left(2x+3\right)}\)
\(=\dfrac{-2\left(x-1\right)\left(x-3\right)}{2x\left(2x-3\right)\left(2x+3\right)}\)
\(=\dfrac{-\left(x-1\right)\left(x-3\right)}{x\left(2x-3\right)\left(2x+3\right)}\)

a)\(\dfrac{3x^2-12x+12}{x^4-8x}=\dfrac{3\left(x^2-4x+4\right)}{x\left(x^3-8\right)}=\dfrac{3\left(x-2\right)^2}{x\left(x^3-2^3\right)}=\dfrac{3\left(x-2\right)^2}{x\left(x-2\right)\left(x^2+2x+4\right)}=\dfrac{3\left(x-2\right)}{x\left(x^2+2x+4\right)}\)

Bài 7:(Sbt/25) Dùng tính chất cơ bản của phân thức hoặc quy tắc đổi dấu để biến mỗi cặp phân thức sau thành một cặp phân thức bằng nó và có cùng mẫu thức :
a. \(\dfrac{3x}{x-5}\) và \(\dfrac{7x+2}{5-x}\)
Ta có:
\(\dfrac{3x}{x-5}=\dfrac{-\left(3x\right)}{-\left(x-5\right)}=\dfrac{-3x}{5-x}\)
\(\dfrac{7x+2}{5-x}\)
Vậy .....
b.\(\dfrac{4x}{x+1}\) và \(\dfrac{3x}{x-1}\)
Ta có:
\(\dfrac{4x}{x+1}=\dfrac{4x\left(x-1\right)}{\left(x+1\right)\left(x-1\right)}=\dfrac{4x^2-4x}{x^2-1}\)
\(\dfrac{3x}{x-1}=\dfrac{3x\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}=\dfrac{3x^2+3x}{x^2-1}\)
Vậy ..........
c. \(\dfrac{2}{x^2+8x+16}\) và \(\dfrac{x-4}{2x+8}\)
Ta có:
\(\dfrac{2}{x^2+8x+16}=\dfrac{4}{2\left(x+4\right)^2}\)
\(\dfrac{x-4}{2x+8}=\dfrac{\left(x-4\right)\left(x+4\right)}{2\left(x+4\right)\left(x+4\right)}=\dfrac{x^2-16}{2\left(x+4\right)^2}\)
Vậy .........
d. \(\dfrac{2x}{\left(x+1\right)\left(x-3\right)}\) và \(\dfrac{x+3}{\left(x+1\right)\left(x-2\right)}\)
Ta có:
\(\dfrac{2x}{\left(x+1\right)\left(x-3\right)}=\dfrac{2x\left(x-2\right)}{\left(x+1\right)\left(x-3\right)\left(x-2\right)}=\dfrac{2x^2-4x}{\left(x+1\right)\left(x-2\right)\left(x-3\right)}\)
\(\dfrac{x+3}{\left(x+1\right)\left(x-2\right)}=\dfrac{\left(x+3\right)\left(x-3\right)}{\left(x+1\right)\left(x-2\right)\left(x-3\right)}=\dfrac{x^2-9}{\left(x+1\right)\left(x-2\right)\left(x-3\right)}\)
Vậy .........

a ) \(\dfrac{x^2+3x+2}{3x+6}=\dfrac{\left(x+1\right)\left(x+2\right)}{3\left(x+2\right)}=\dfrac{x+1}{3}\) (1)
\(\dfrac{2x^2+x-1}{6x-3}=\dfrac{\left(2x-1\right)\left(x+1\right)}{3\left(2x-1\right)}=\dfrac{x+1}{3}\) (2)
Từ (1) ; (2) \(\Rightarrow\dfrac{x^2+3x+2}{3x+6}=\dfrac{2x^2+x-1}{6x-3}\) (đpcm)
b ) \(\dfrac{15x-10}{3x^2+3x-\left(2x+2\right)}=\dfrac{5\left(3x-2\right)}{\left(3x-2\right)\left(x+1\right)}=\dfrac{5}{x+1}\) (3)
\(\dfrac{5x^2-5x+5}{x^3+1}=\dfrac{5\left(x^2-x+1\right)}{\left(x+1\right)\left(x^2-x+1\right)}=\dfrac{5}{x+1}\) (4)
Từ (3) và (4) \(\Rightarrow\dfrac{15x-10}{3x^2+3x-\left(2x+2\right)}=\dfrac{5x^2-5x+5}{x^3+1}\) (đpcm)
a) \(\dfrac{x^2+3x+2}{3x+6}=\dfrac{x^2+x+2x+2}{3\left(x+2\right)}=\dfrac{\left(x^2+x\right)+\left(2x+2\right)}{3\left(x+2\right)}=\dfrac{x\left(x+1\right)+2\left(x+1\right)}{3\left(x+2\right)}=\dfrac{\left(x+1\right)\left(x+2\right)}{3\left(x+2\right)}=\dfrac{x+1}{3}\left(1\right)\) \(\dfrac{2x^2+x-1}{6x-3}=\dfrac{2x^2+2x-x-1}{3\left(2x-1\right)}=\dfrac{2x\left(x+1\right)-\left(x+1\right)}{3\left(2x-1\right)}=\dfrac{\left(2x-1\right)\left(x+1\right)}{3\left(2x-1\right)}=\dfrac{x+1}{3}\left(2\right)\) Từ (1)và (2)=> \(\dfrac{x^2+3x+2}{3x+6}=\dfrac{2x^2+x-1}{6x-3}\) b)\(\dfrac{15x-10}{3x^2+3x-\left(2x+2\right)}=\dfrac{5\left(3x-2\right)}{3x\left(x+1\right)-2\left(x+1\right)}=\dfrac{5\left(3x-2\right)}{\left(3x-2\right)\left(x+1\right)}=\dfrac{5}{x+1}\left(3\right)\) \(\dfrac{5x^2-5x+5}{x^3+1}=\dfrac{5\left(x^2-x+1\right)}{\left(x+1\right)\left(x^2-x+1\right)}=\dfrac{5}{x+1}\left(4\right)\) Từ (3) và (4) => \(\dfrac{15x-10}{3x^2+3x-\left(2x+2\right)}=\dfrac{5x^2-5x+5}{x^3+1}\)

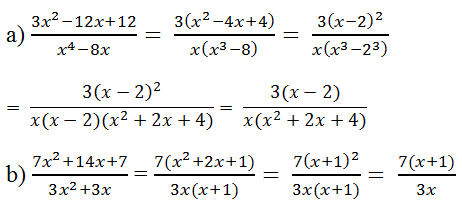
Giải bằng phương pháp hệ số bất định:
Ta có: \(3x^2+x-14=3x^2-6x+7x-14\)
\(=\left(x-2\right)\left(3x+7\right)\) nên \(C=\dfrac{17x+18}{\left(x-2\right)\left(3x+7\right)}\)
Ta có : \(\dfrac{a}{x-2}+\dfrac{b}{3x+7}=\dfrac{a\left(3x+7\right)+b\left(x-2\right)}{\left(x-2\right)\left(3x+7\right)}\)
Khai triển trên tử ra , ta có:
\(=\dfrac{\left(3a+b\right)x+\left(7a-2b\right)}{\left(x-2\right)\left(3x+7\right)}\)
Như vậy ta có: 17x+18 = (3a+b) x + (7a-2b) với mọi x;
Đồng nhất hệ số các hạng tử cùng bậc ở 2 vế ta có:
\(\left\{{}\begin{matrix}3a+b=7\\7a-2b=18\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=4\\b=5\end{matrix}\right.\)
CHÚC BẠN HỌC TỐT...
Bạn chỉ cần phân tích phân thức C thành tổng của hai phân thức kia , rồi xem số đó là bao nhiêu rồi thay a , b vào thôi .