HT
3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
23 tháng 3 2019
\(2x^3+x^2+x-1=0\)
\(\Rightarrow2x^3-x^2+2x^2-x+2x-1=0\)
\(\Rightarrow x^2\left(2x-1\right)+x\left(2x-1\right)+2x-1=0\)
\(\Rightarrow\left(2x-1\right)\left(x^2+x+1\right)=0\)
Mà \(x^2+x+1=x^2+\frac{1}{2}x+\frac{1}{2}x+\frac{1}{4}+\frac{3}{4}\)
\(=x\left(x+\frac{1}{2}\right)+\frac{1}{2}\left(x+\frac{1}{2}\right)+\frac{3}{4}=\left(x+\frac{1}{2}\right)^2+\frac{3}{4}>0\)
Do đó: \(2x-1=0\Rightarrow x=\frac{1}{2}\) (loại vì \(x\notin Z\))
Vậy đa thức C không có nghiệm nguyên
(phần tách C thành tích các đa thức chính là \(\left(2x-1\right)\left(x^2+x+1\right)\) )
HP
19 tháng 5 2016
a)Vì T(x)=P(x)+Q(x)
=>T(x)=(-2x2-5x+1)+(-2x2+x-5)
=>T(x)=-2x2-5x+1-2x2+x-5
=>T(x)=(-2x2-2x2)+(-5x+x)+(1-5)=-4x2-4x-4
b)Xét T(x)=-4x2-4x-4=0
=>-(4x2+4x+4)=0
=>4x2+4x+4=0
=>4x2+2x+2x+1+3=0
=>2x(2x+1)+(2x+1)+3=0
=>(2x+1)(2x+1)+3=0
=>(2x+1)2+3=0
Vì (2x+1)2 > 0 với mọi x
=>(2x+1)2+3 > 3 > 0 với mọi x
=>T(x) vô nghiệm
H
19 tháng 4 2017
a) Ta có: P(x) = 0 khi 3 – 2x = 0
=>-2x = -3 => x = \(\dfrac{3}{2}\)
b) Q(x) =x2 +2 là đa thức không có nghiệm vì
x2 ≥ 0
2 > 0 (theo quy tắc nhân hai số hữu tỉ cùng dấu)
=>x2 + 2 > 0 với mọi x
Nên Q(x) không có nghiệm trong R
TP
19 tháng 4 2017
a) Ta có P(x) = 0 khi 3 – 2x = 0
b) Đa thức Q(x) không có nghiệm, bởi vì:
x2 ≥ 0 với mọi x thuộc R.
2 > 0
\(\Rightarrow\) Q(x) = x2 + 2 > 0 với mọi x thuộc R.
Do đó, không có giá trị x nào thuộc R để Q(x) = 0 hay đa thức Q(x) không có nghiệm.
23 tháng 4 2019
a)
\(x^2-5x+4=x^2+x-4x+4=x\left(x+1\right)-4\left(x+1\right)=\left(x+1\right)\left(x-4\right)\)
Để đa thức có nghiệm thì \(\left(x+1\right)\left(x-4\right)=0\)
\(\Rightarrow\orbr{\begin{cases}x+1=0\\x-4=0\end{cases}}\Rightarrow\orbr{\begin{cases}x=-1\\x=4\end{cases}}\)
b)
\(x+2x^2=x\left(1+2x\right)=0\)
\(\Rightarrow\orbr{\begin{cases}x=0\\1+2x=0\end{cases}}\Rightarrow\orbr{\begin{cases}x=0\\x=-\frac{1}{2}\end{cases}}\)
c)
\(x\left(x-1\right)-x\left(x+3\right)+4\)
\(=x\left(x-1-x-3\right)+4\)
\(=-4x+4\)
Đa thức có nghiệm khi:\(-4\left(x+1\right)=0\)
\(\Leftrightarrow x=-1\)
21 tháng 4 2017
a) A(x)= \(-2x^4+x^2-x-7-2\)
B(x)=\(2x^4+6x^3-2x^3-x^2-8x-5\)
b) Thay số:A(x)
\(1^2-1-2-2\cdot1^4+7=3\)
B(x)
\(6\cdot2^3+2\cdot2^4-8\cdot2-5-2\cdot2^3-2^2=39\)
c)\(6x^3-2x^3-7x-12-2\)
14 tháng 8 2017
1. Thay x = -2 vào \(f\left(x\right)\), ta có:
\(\left(-2\right)^3+2.\left(-2\right)^2+a.\left(-2\right)+1=\)0
=> -8 + 8 - 2a + 1 = 0
=> -2a +1 = 0
=> -2a = -1
=> a = \(\frac{1}{2}\)
Vậy a = \(\frac{1}{2}\)
2. * Thay x = 1 vào \(f\left(x\right)\), ta có:
12 + 1.a + b = 1 + a + b = 0 ( 1)
* Thay x = 2 vào biểu thức \(f\left(x\right)\), ta có:
22 + 2.a + b = 4 + 2a + b = 0 ( 2)
* Lấy (2 ) - ( 1) , ta có:
( 4 + 2a + b ) - ( 1 + a + b ) = 3 + a
=> 3 + a = 0
=> a = -3
* 1 + a + b = 0
=> 1 - 3 + b = 0
=> b = -1 + 3 = -2
Vậy a= -3 và b= -2
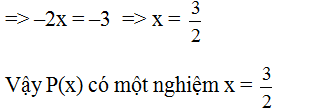
Đặt A(x)=0
\(\Leftrightarrow x^3-2x=0\)
\(\Leftrightarrow x\left(x^2-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x^2-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\sqrt{2}\\x=-\sqrt{2}\end{matrix}\right.\)
Vậy: \(S=\left\{0;\sqrt{2};-\sqrt{2}\right\}\)
A(x)= x3 - 2x
Cho A(x) = 0
=> x3 - 2x = 0
x ( x2 - 2 ) = 0
x = 0 hoặc x2 -2 = 0
x 2 = 2
x = \(\sqrt{2}\) hoặc x = \(-\sqrt{2}\)
Vậy x = 0 hoặc x = \(\sqrt{2}\) hoặc x = \(-\sqrt{2}\) là nghiệm của đa thức A(x)