Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có 3x^2-x+1=3x^2+2x-3x-2+3=(3x-2)(x-1)+3
D có giá trị nguyên\(\) khi 3\(⋮\)(3x+2)\(\Leftrightarrow\)3x+2 là ước của 3\(\Leftrightarrow\)3x+2\(\in\){-3;-1;1;3} suy ra x\(\in\){-5/3;-1;-1/3;1/3}mà x nguyên nên ta tìm được x=-1

a) \(x\ne2\) ; \(x\ne-2\)
b) Ta có
\(C=\frac{x^3}{x^2-4}-\frac{x}{x-2}-\frac{2}{x+2}=\frac{x^3}{\left(x-2\right)\left(x+2\right)}-\frac{x}{x-2}-\frac{2}{x+2}\)
\(=\frac{x^3-x.\left(x+2\right)-2.\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}=\frac{x^3-x^2-2x-2x+4}{\left(x-2\right)\left(x+2\right)}=\frac{x^2.\left(x-1\right)-4.\left(x-1\right)}{x^2-4}\)
\(=\frac{\left(x-1\right)\left(x^2-4\right)}{x^2-4}=x-1\)
Để C = 0 thì x-1 = 0 =>>> x=1(tm)
c) Để C nhận giá trị dương thì C thuộc Z+ = >>>>>>>> \(x-1\ge0\)=>>> \(x\ge1\)

a) ĐKXĐ: x ≠ 0; x ≠ -1; x ≠ 1/2.
Rút gọn được A = (x - 1)/3
b) Từ 2014 - |2x - 1| = 2013
Tìm được x = 1; x = 0 (loại x = 0 do không thỏa mãn ĐK)
Thay x = 1 vào biểu thức. Tính được A = 0.
c) A< 0 suy luận được x<1 và : x ≠ 0; x ≠ -1; x ≠ 1/2 .
d) Lập luận để khẳng định được x-1 là bội của 3 suy ra , x = 3n+1 (n ∈ Z)

Đặt tính \(2n^2-n+2\) : \(2n+1\) sẽ bằng n - 1 dư 3
Để chia hết thì 3 phải chia hết cho 2n + 1 hay 2n + 1 là ước của 3
Ư(3) = {\(\pm\) 3; \(\pm\) 1}
\(2n+1=1\Leftrightarrow2n=0\Leftrightarrow n=0\)
\(2n+1=-1\Leftrightarrow2n=-2\Leftrightarrow n=-1\)
\(2n+1=3\Leftrightarrow2n=2\Leftrightarrow n=1\)
\(2n+1=-3\Leftrightarrow2n=-4\Leftrightarrow n=-2\)
Vậy \(n=\left\{0;-2;\pm1\right\}\)

ta có : \(m=x^2-x+1=x^2-2.\dfrac{1}{2}.x+\left(\dfrac{1}{2}\right)^2+\dfrac{3}{4}=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\) với mọi \(x\)
\(\Rightarrow\) giá trị nhỏ nhất của \(m=x^2-x+1\) là \(\dfrac{3}{4}\) khi \(\left(x-\dfrac{1}{2}\right)^2=0\Leftrightarrow x-\dfrac{1}{2}=0\Leftrightarrow x=\dfrac{1}{2}\)
vậy giá trị nhỏ nhất của \(m=x^2-x+1\) là \(\dfrac{3}{4}\) khi \(x=\dfrac{1}{2}\)

Để A nguyên thì \(x^2-x+4x-4+9⋮x-1\)
\(\Leftrightarrow x-1\in\left\{1;-1;3;-3;9;-9\right\}\)
hay \(x\in\left\{2;0;4;-2;10;-8\right\}\)

\(A=\dfrac{3x^3-4x^2+x-1}{x-4}=\dfrac{3x^2\left(x-4\right)+8x\left(x-4\right)+33\left(x-4\right)+131}{x-4}=\dfrac{\left(x-4\right)\left(3x^2+8x+33\right)+131}{x-4}=3x^2+8x+33+\dfrac{131}{x-4}\in Z\)
\(\Rightarrow\left(x-4\right)\inƯ\left(131\right)=\left\{-131;-1;1;131\right\}\)
\(\Rightarrow x\in\left\{-127;3;5;135\right\}\)

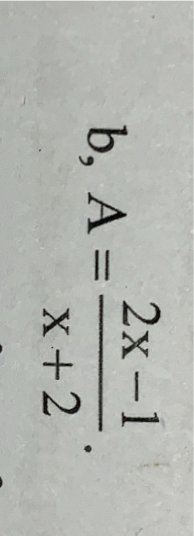
\(A=\dfrac{2x-1}{x+2}\)
\(\Rightarrow A=\dfrac{2x+4-5}{x+2}\)
\(\Rightarrow A=\dfrac{2\left(x+2\right)-5}{x+2}\)
\(\Rightarrow A=\dfrac{2\left(x+2\right)}{x+2}-\dfrac{5}{x+2}\)
\(\Rightarrow A=2-\dfrac{5}{x+2}\)
\( Để.A\in Z.mà.2\in Z\Rightarrow\dfrac{5}{x+2}\in Z\Rightarrow5⋮\left(x+2\right)\Rightarrow x+2\inƯ\left(5\right)=\left\{\pm1;\pm5\right\}\)
Ta có bảng:
| x+2 | -1 | -5 | 1 | 5 |
| x | -3 | -7 | -1 | 3 |
Vậy \(x\in\left\{-3;-7;-1;3\right\}\)

Sau khi ib với Đinh Lan Anh thì \(P=\frac{2a^2}{a^2-1}+\frac{a}{a+1}-\frac{a}{a-1}\)
\(a,ĐKXĐ:\hept{\begin{cases}a+1\ne0\\a-1\ne0\end{cases}\Leftrightarrow a\ne\pm1}\)
\(b,P=\frac{2a^2}{a^2-1}+\frac{a}{a+1}-\frac{a}{a-1}\)
\(=\frac{2a^2+a\left(a-1\right)-a\left(a+1\right)}{\left(a-1\right)\left(a+1\right)}\)
\(=\frac{2a^2+a^2-a-a^2-q}{\left(a-1\right)\left(a+1\right)}\)
\(=\frac{2a^2-2a}{\left(a-1\right)\left(a+1\right)}\)
\(=\frac{2a\left(a-1\right)}{\left(a-1\right)\left(a+1\right)}\)
\(=\frac{2a}{a+1}\)
\(c,P=\frac{2a}{a+1}=\frac{2a+2}{a+1}-\frac{2}{a+1}=2-\frac{2}{a+1}\)
Để \(P\inℤ\)thì \(2-\frac{2}{a+1}\inℤ\)
\(\Leftrightarrow\frac{2}{a+1}\inℤ\)
Mà \(a\inℤ\Rightarrow a+1\inℤ\)
Ta có bảng
| a + 1 | -2 | -1 | 1 | 2 |
| a | -3 | -2 | 0 | 1 |
Kết hợp ĐKXĐ \(a\ne\pm1\)ta được \(a\in\left\{-3;-2;0\right\}\)
Vậy //////
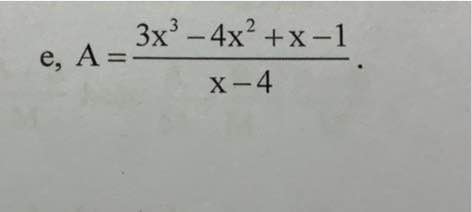



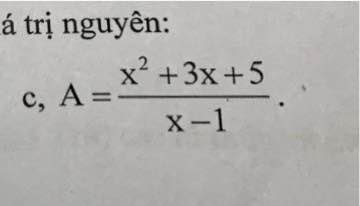
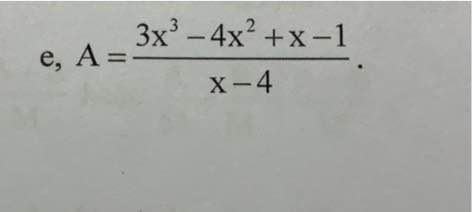

Để A nguyên thì \(3x^3-12x^2+8x^2-32x+33x-132+131⋮x-4\)
\(\Leftrightarrow x-4\in\left\{1;-1;131;-131\right\}\)
hay \(x\in\left\{5;3;135;-127\right\}\)