Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Từ trường hợp 1 ta có:
- Nếu cạnh bên và cạnh dáy của tam giác cân này tỉ lệ với cạnh bên và cạnh đáy của tam giác cân kia thì hai tam giác đó đồng dạng.
Từ trường hợp 2 và 3 ta nói:
- Nếu hai tam giác cân có một góc tương ứng bằng nhau thì hai tam giác đó đồng dạng.
Từ trường hợp 1 ta có:
- Nếu cạnh bên và cạnh đáy của tam giác cân này tỉ lệ với cạnh bên và cạnh đáy của tam giác cân kia thì hai tam giác đó đồng dạng.
Từ trường hợp 2 và 3 ta có:
- Nếu hai tam giác cân có một góc tương ứng bằng nhau thì hai tam giác đó đồng dạng.

+ Nếu cạnh bên và cạnh đáy của tam giác cân này tỉ lệ với cạnh bên và cạnh đáy của tam giác cân kia thì hai tam giác đó đồng dạng.
+ Nếu hai tam giác cân có hai góc ở đỉnh bằng nhau thì hai tam giác cân đồng dạng.
+ Nếu góc ở đáy của tam giác cân này bằng góc ở đáy của tam giác cân kia thì hai tam giác cân đó đồng dạng.

Từ trường hợp 1 ta có:
- Nếu cạnh bên và cạnh dáy của tam giác cân này tỉ lệ với cạnh bên và cạnh đáy của tam giác cân kia thì hai tam giác đó đồng dạng.
Từ trường hợp 2 và 3 ta nói:
- Nếu hai tam giác cân có một góc tương ứng bằng nhau thì hai tam giác đó đồng dạng.
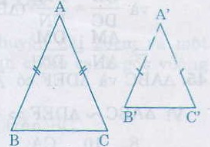
Từ trường hợp 1 ta có:
- Nếu cạnh bên và cạnh dáy của tam giác cân này tỉ lệ với cạnh bên và cạnh đáy của tam giác cân kia thì hai tam giác đó đồng dạng.
Từ trường hợp 2 và 3 ta nói:
- Nếu hai tam giác cân có một góc tương ứng bằng nhau thì hai tam giác đó đồng dạng.

Hướng dẫn cách hack VIP OLM Vĩnh Viễn siêu dễ chỉ 10 phút là xong: youtube.com/watch?v=zYcnHqUcGZE&t

Cho a',b',c' là số đo cạnh của tam giác A'B'C'
a,b,c là số đo cạnh của tam giác ABC
a) Theo đề bài ta có: \(\frac{a'}{a}=\frac{b'}{b}=\frac{c'}{c}=k=\frac{3}{5}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có: \(\frac{a'}{a}=\frac{b'}{b}=\frac{c'}{c}=\frac{a'+b'+c'}{a+b+c}=\frac{P_{A'B'C'}}{P_{ABC}}=k=\frac{3}{5}\)
Vậy tỉ số chu vi hai tam giác đã cho là 3/5
b) Chu vi tam giác ABC là: \(P_{ABC}=40:\left(5-3\right)\cdot5=100\left(dm\right)\)
Chu vi tam giác A'B'C' là: \(P_{A'B'C'}=P_{ABC}-40dm=100dm-40dm=60\left(dm\right)\)
A B C A' B' C'
a, Gọi CV tam giác A'B'C' là P', ABC là P
\(\Delta A'B'C'~\Delta ABC\)theo tỉ số đồng dạng \(k=\frac{3}{5}\)
\(\Rightarrow\frac{A'B'}{AB}=\frac{B'C'}{BC}=\frac{C'A'}{CA}=\frac{3}{5}\)
Áp dụng t/c DTSBN , ta có :
\(\frac{3}{5}=\frac{A'B'}{AB}=\frac{B'C'}{BC}=\frac{C'A'}{CA}\)
\(=\frac{A'B'+B'C'+C'A'}{AB+BC+CA}=\frac{P'}{P}\)
Vậy tỉ số chu vi tam giác A'B'C' và ABC là \(\frac{3}{5}\)
+ Nếu cạnh bên và cạnh đáy của tam giác cân này tỉ lệ với cạnh bên và cạnh đáy của tam giác cân kia thì hai tam giác đó đồng dạng.
+ Nếu hai tam giác cân có hai góc ở đỉnh bằng nhau thì hai tam giác cân đồng dạng.
+ Nếu góc ở đáy của tam giác cân này bằng góc ở đáy của tam giác cân kia thì hai tam giác cân đó đồng dạng.