Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn viết lại đề được ko? Ko hiểu \(\frac{x'+x}{x}\) với \(x\ne0\) là gì
Các câu dưới cũng có kí hiệu này, chắc bạn viết nhầm sang kí hiệu nào đó, nó cũng ko phải kí hiệu đạo hàm

\(\lim\limits_{x\rightarrow0}\left|f\left(x\right)\right|=\lim\limits_{x\rightarrow0}\left|x^2sin\dfrac{1}{x}\right|< \lim\limits_{x\rightarrow0}\left|x^2\right|=0\).
Vậy \(\lim\limits_{x\rightarrow0}f\left(x\right)=0\).
\(f\left(0\right)=A\).
Để hàm số liên tục tại \(x=0\) thì \(\lim\limits_{x\rightarrow0}f\left(x\right)=f\left(0\right)\Leftrightarrow A=0\).
Để xét hàm số có đạo hàm tại \(x=0\) ta xét giới hạn:
\(\lim\limits_{x\rightarrow0}\dfrac{f\left(x\right)-f\left(0\right)}{x-0}=\lim\limits_{x\rightarrow0}\dfrac{x^2sin\dfrac{1}{x}}{x}=\lim\limits_{x\rightarrow0}xsin\dfrac{1}{x}=0\).
Vậy hàm số có đạo hàm tại \(x=0\).

d/
\(f'\left(x\right)=4cos^2\frac{x}{2}-2x.2cos\frac{x}{2}.sin\frac{x}{2}=2\left(1+cosx\right)-2x.sinx\)
\(f'\left(x\right)=g\left(x\right)\)
\(\Leftrightarrow2+2cosx-2x.sinx=8cos\frac{x}{2}-3-2sinx\)
Chà, có vẻ bạn ghi ko đúng đề, pt này ko giải được.
Chắc \(g\left(x\right)=8cos\frac{x}{2}-3-2x.sinx\) mới đúng chứ nhỉ?
c/
\(f'\left(x\right)=4x.cos^2\frac{x}{2}-2x^2.cos\frac{x}{2}.sin\frac{x}{2}=2x\left(1+cosx\right)-x^2sinx\)
\(f'\left(x\right)=g\left(x\right)\)
\(\Leftrightarrow2x\left(1+cosx\right)-x^2sinx=x-x^2sinx\)
\(\Leftrightarrow2x\left(1+cosx\right)=x\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\2\left(1+cosx\right)=1\left(1\right)\end{matrix}\right.\)
\(\left(1\right)\Leftrightarrow cosx=-\frac{1}{2}\)
\(\Rightarrow\left[{}\begin{matrix}x=\frac{2\pi}{3}+k2\pi\\x=-\frac{2\pi}{3}+k2\pi\end{matrix}\right.\)

a) Cách 1: Ta có:
y' = 6sin5x.cosx - 6cos5x.sinx + 6sinx.cos3x - 6sin3x.cosx = 6sin3x.cosx(sin2x - 1) + 6sinx.cos3x(1 - cos2x) = - 6sin3x.cos3x + 6sin3x.cos3x = 0.
Vậy y' = 0 với mọi x, tức là y' không phụ thuộc vào x.
Cách 2:
y = sin6x + cos6x + 3sin2x.cos2x(sin2x + cos2x) = sin6x + 3sin4x.cos2x + 3sin2x.cos4x + cos6x = (sin2x + cos2x)3 = 1
Do đó, y' = 0.
b) Cách 1:
Áp dụng công thức tính đạo hàm của hàm số hợp
(cos2u)' = 2cosu(-sinu).u' = -u'.sin2u
Ta được
y' =[sin - sin
] + [sin
- sin
] - 2sin2x = 2cos
.sin(-2x) + 2cos
.sin(-2x) - 2sin2x = sin2x + sin2x - 2sin2x = 0,
vì cos = cos
=
.
Vậy y' = 0 với mọi x, do đó y' không phụ thuộc vào x.
Cách 2: vì côsin của hai cung bù nhau thì đối nhau cho nên
cos2 = cos2
'
cos2 = cos2
.
Do đó
y = 2 cos2 + 2cos2
- 2sin2x = 1 +cos
+ 1 +cos
- (1 - cos2x) = 1 +cos
+ cos
+ cos2x = 1 + 2cos
.cos(-2x) + cos2x = 1 + 2
cos2x + cos2x = 1.
Do đó y' = 0.

Bài 1:
\(\lim\limits_{x\rightarrow1}f\left(x\right)=\lim\limits_{x\rightarrow1}\frac{\sqrt{x+3}-2+2-\sqrt[3]{3x+5}}{x-1}=\lim\limits_{x\rightarrow1}\frac{\frac{x-1}{\sqrt{x+3}+2}-\frac{3\left(x-1\right)}{4+2\sqrt[3]{3x+5}+\sqrt[3]{\left(3x+5\right)^2}}}{x-1}\)
\(=\lim\limits_{x\rightarrow1}\left(\frac{1}{\sqrt{x+3}+2}-\frac{3}{4+2\sqrt[3]{3x+5}+\sqrt[3]{\left(3x+5\right)^2}}\right)=0\)
\(f\left(1\right)=a+1\)
Để hàm số liên tục trên \([-3;+\infty)\Leftrightarrow\) hàm số liên tục tại \(x=1\)
\(\Leftrightarrow\lim\limits_{x\rightarrow1}f\left(x\right)=f\left(1\right)\Rightarrow a+1=0\Rightarrow a=-1\)
Bài 2:
Các hàm số đã cho đều liên tục trên R nên liên tục trên từng khoảng bất kì
a/ Xét \(f\left(x\right)=m\left(x-1\right)^3\left(x+2\right)+2x+3\)
\(f\left(-2\right)=-1\) ; \(f\left(1\right)=5\)
\(\Rightarrow f\left(-2\right).f\left(1\right)< 0;\forall m\)
\(\Rightarrow f\left(x\right)\) luôn có ít nhất 1 nghiệm thuộc \(\left(-2;1\right)\) với mọi m
b/ \(m\left(sin^3x-cosx\right)=0\)
Nếu \(m=0\) pt có vô số nghiệm (thỏa mãn)
Nếu \(m\ne0\Leftrightarrow f\left(x\right)=sin^3x-cosx=0\)
\(f\left(0\right)=-1\) ; \(f\left(\frac{\pi}{2}\right)=1\)
\(\Rightarrow f\left(0\right).f\left(\frac{\pi}{2}\right)< 0\)
\(\Rightarrow f\left(x\right)\) luôn có ít nhất 1 nghiệm thuộc \(\left(0;\frac{\pi}{2}\right)\)
Phương trình luôn có nghiệm với mọi m

Chứng minh các biểu thức đã cho không phụ thuộc vào x.
Từ đó suy ra f'(x)=0
a) f(x)=1⇒f′(x)=0f(x)=1⇒f′(x)=0 ;
b) f(x)=1⇒f′(x)=0f(x)=1⇒f′(x)=0 ;
c) f(x)=\(\frac{1}{4}\)(\(\sqrt{2}\)-\(\sqrt{6}\))=>f'(x)=0
d,f(x)=\(\frac{3}{2}\)=>f'(x)=0

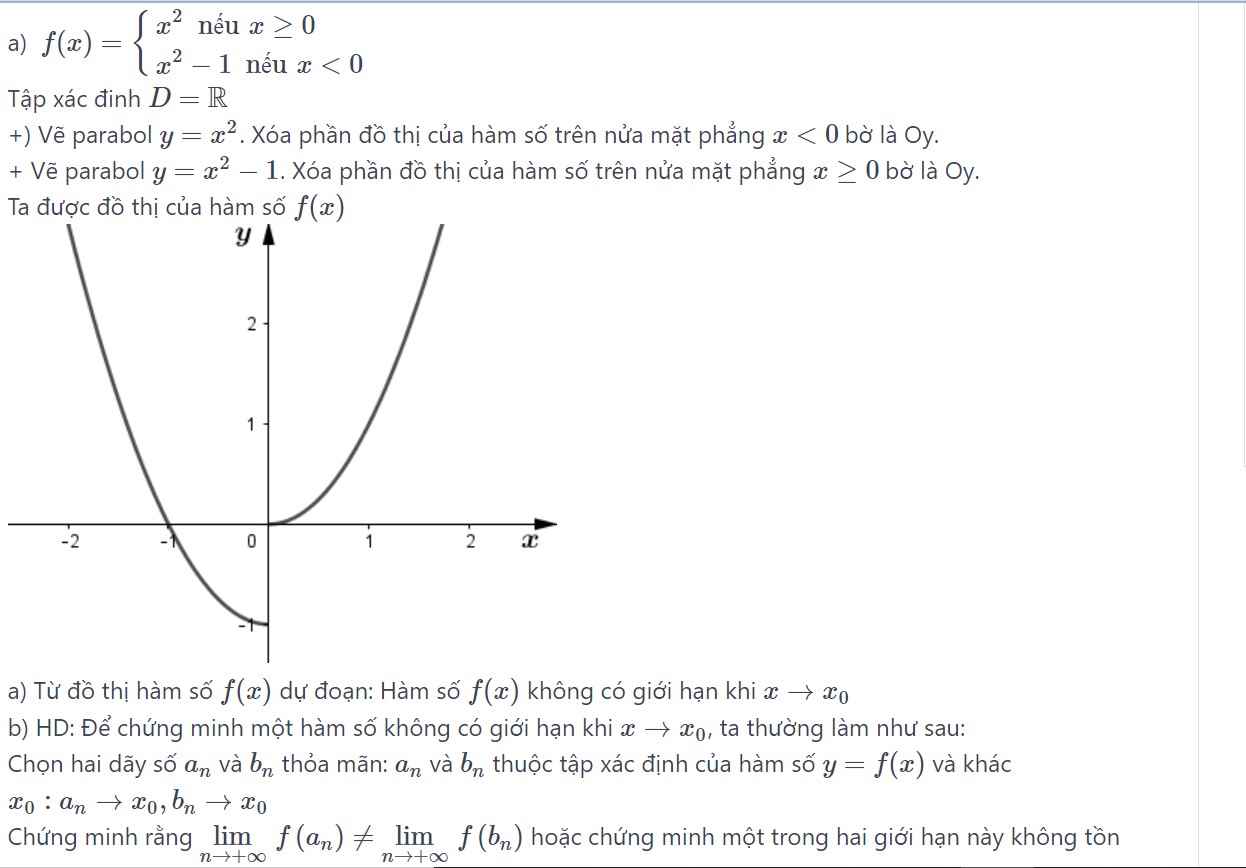
a) Các bạn tự vẽ hình nhé . Đồ thị hàm số y = f(x) là một đường không liền nét mà bị đứt quãng tại x0 = -1. Vậy hàm số đã cho liên tục trên khoảng (-∞; -1) và (- 1; +∞).
b) +) Nếu x < -1: f(x) = 3x + 2 liên tục trên (-∞; -1) (vì đây là hàm đa thức).
+) Nếu x> -1: f(x) = x2 – 1 liên tục trên (-1; +∞) (vì đây là hàm đa thức).
+) Tại x = -1;
Ta có =![]() = 3(-1) +2 = -1.
= 3(-1) +2 = -1.
![]() = (-1)2 – 1 = 0.
= (-1)2 – 1 = 0.
Vì ![]() nên không tồn tại
nên không tồn tại  . Vậy hàm số gián đoạn tại
. Vậy hàm số gián đoạn tại
x0 = -1.
TenAnh1 TenAnh1 A = (-0.04, -7.12) A = (-0.04, -7.12) A = (-0.04, -7.12) B = (15.32, -7.12) B = (15.32, -7.12) B = (15.32, -7.12) D = (10.58, -5.6) D = (10.58, -5.6) D = (10.58, -5.6)
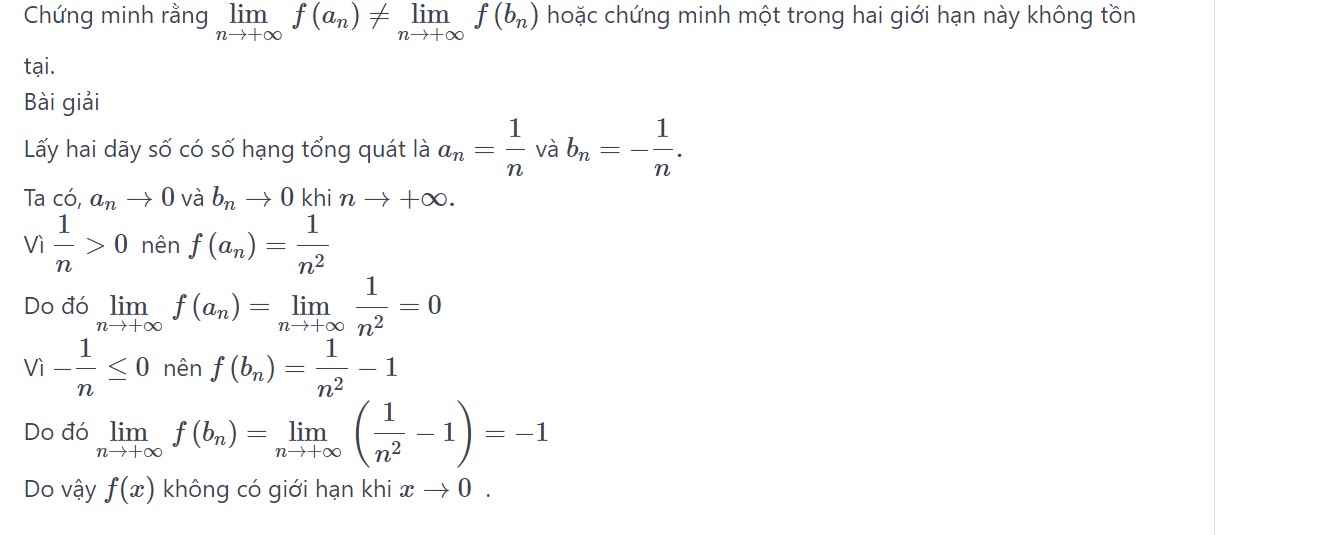
Giá trị của \(f\left(-x\right)\) và \(f\left(x\right)\) khi \(x=0\) phải bằng nhau
Bạn thay \(x=0\) vào 2 biểu thức chứa dấu "=" là ra đẳng thức đó thôi
\(f\left(-x\right)=\left\{{}\begin{matrix}\left(1-3a\right)sinx+b.cosx,khi.x>0\\-a.sinx+\left(3-2b\right)cosx,khi.x\le0\end{matrix}\right.\)
Hàm đã cho là hàm lẻ khi và chỉ khi:
\(\left\{{}\begin{matrix}b=3-2b\\\left(3a-1\right)sinx+b.cosx=-a.sinx+\left(3-2b\right)cosx\\a.sinx+\left(3-2b\right)cosx=\left(1-3a\right)sinx+b.cosx\end{matrix}\right.\) \(\forall x\)
\(\Leftrightarrow\left\{{}\begin{matrix}b=1\\\left(4a-1\right)sinx+\left(3b-3\right)cosx=0\\\left(4a-1\right)sinx+\left(3-3b\right)cosx=0\end{matrix}\right.\) ;\(\forall x\)
\(\Leftrightarrow\left\{{}\begin{matrix}b=1\\4a-1=0\\3b-3=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}a=\frac{1}{4}\\b=1\end{matrix}\right.\)