K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
DK
1
8 tháng 1 2021
Không mất tính tổng quát giả sử \(a\le b\).
Nếu a = 0 thì (a, b) = b; [a, b] = 0 nên b = 26.
Xét a khác 0.
Đặt \(\left(a,b\right)=d\Rightarrow\left\{{}\begin{matrix}a=da'\\b=db'\end{matrix}\right.\) với (a', b') = 1; \(a'\le b'\).
Khi đó \(\left[a,b\right]=da'b'\).
Từ đề bài suy ra: \(d+da'b'=26\Leftrightarrow d\left(a'b'+1\right)=26\).
Do d, a', b' là các số tự nhiên nên ta có các trường hợp:
+) \(\left\{{}\begin{matrix}d=1\\a'b'=25\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}d=1\\a'=1;b'=25\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}a=1\\b=25\end{matrix}\right.\).
+) \(\left\{{}\begin{matrix}d=2\\a'b'=12\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}d=2\\\left[{}\begin{matrix}a'=1;b'=12\\a'=3;b'=4\end{matrix}\right.\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}a=2;b=24\\a=6;b=8\end{matrix}\right.\).
+) \(\left\{{}\begin{matrix}d=13\\a'b'=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}d=13\\a'=1;b'=1\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}a=13\\b=13\end{matrix}\right.\).
Vậy...
LD
0
NX
0
H
2 tháng 8 2016
Gọi M là chân đg trung tuyến hạ từ B đến AC
=>M(t,\(\frac{9t-7}{5}\) )
=>C(2t-2,\(\frac{18t-19}{5}\) )
pt AH:2x+3y-7=0
Do C=BC vuông với AH =>15x-10y+6t-8=0
Tọa độ đỉnh B là nghiệm của hệ \(\begin{cases}9x-5y-7=0\\15x-10y+6t-8=0\end{cases}\) =>B(2t+2,\(\frac{18t+11}{5}\) )
Lại có BH vuông với AC =>BH*AC=0
=>t=?
25 tháng 1 2021
2: Điểm rơi... đẹp!
Áp dụng bất đẳng thức AM - GM:
\(\left\{{}\begin{matrix}a^2+1\ge2a\\b^2+4\ge4b\\c^2+9\ge6c\end{matrix}\right.\)
\(\Rightarrow a^2+b^2+c^2+14\ge2\left(a+2b+3c\right)=28\).
\(\Rightarrow a^2+b^2+c^2\ge14\).
Đẳng thức xảy ra khi a = 1; b = 2; c = 3.
25 tháng 1 2021
1: Ta có \(y^2\ge6-x+x-2=4\Rightarrow y\ge2\).
Đẳng thức xảy ra khi x = 6 hoặc x = 2
\(y^2\le2\left(6-x+x-2\right)=8\Rightarrow y\le2\sqrt{2}\).
Đẳng thức xảy ra khi x = 4.
11 tháng 12 2020
Ủa phải là vt a ⊥ vt b chứ tao hong thì góc giữa chúng là 90 độ ròi
NV
Nguyễn Việt Lâm
Giáo viên
25 tháng 5 2020
d/ \(B=180^0-\left(A+C\right)=75^0\)
\(\Rightarrow b=c=4,5\)
\(\frac{a}{sinA}=\frac{b}{sinB}\Rightarrow a=\frac{b.sinA}{sinB}=\frac{9}{4}\left(\sqrt{6}-\sqrt{2}\right)\)
e/ \(cosA=\frac{b^2+c^2-a^2}{2bc}\Rightarrow a=\sqrt{b^2+c^2-2bc.cosA}\approx23\)
\(cosB=\frac{a^2+c^2-b^2}{2ac}=\frac{433}{460}\Rightarrow B\approx19^043'\)
\(\Rightarrow C=180^0-\left(A+B\right)=...\)
f/ \(cosA=\frac{b^2+c^2-a^2}{2bc}=\frac{11}{15}\Rightarrow A\approx42^050'\)
\(cosB=\frac{a^2+c^2-b^2}{2ac}=\frac{17}{35}\Rightarrow B\approx60^056'\)
\(C=180^0-\left(A+B\right)=...\)
NV
Nguyễn Việt Lâm
Giáo viên
25 tháng 5 2020
a/ \(cosA=\frac{b^2+c^2-a^2}{2bc}=-\frac{1}{2}\Rightarrow A=120^0\)
\(cosB=\frac{a^2+c^2-b^2}{2ac}=\frac{\sqrt{2}}{2}\Rightarrow B=45^0\)
\(C=180^0-\left(A+B\right)=15^0\)
b/\(A=180^0-\left(B+C\right)=79^037'\)
\(\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}\Rightarrow\left\{{}\begin{matrix}b=\frac{sinB}{sinA}.a\approx61\\c=\frac{sinC}{sinA}.a\approx102\end{matrix}\right.\)
c/\(\frac{a}{sinA}=\frac{b}{sinB}\Rightarrow sinB=\frac{bsinA}{a}\approx0,6\Rightarrow B\approx36^052'\)
\(\Rightarrow C=180^0-\left(A+B\right)=75^045'\)
\(\frac{a}{sinA}=\frac{c}{sinC}\Rightarrow c=\frac{a.sinC}{sinA}\approx21\)
LH
Câu 14: cho khoảng A = ( -∞ ; 6 / 2-m ) và khoảng B=(1-m ; + ∞ ) tìm tất cả các số thực để A \ B = A
1
11 tháng 12 2023
ĐKXĐ: m<>2
Để A\B=A thì A giao B=rỗng
Để \(A\cap B=\varnothing\) thì \(\dfrac{6}{2-m}< =1-m\)
=>\(\dfrac{6-\left(1-m\right)\left(2-m\right)}{2-m}< =0\)
=>\(\dfrac{6-\left(m-2\right)\left(m-1\right)}{m-2}>=0\)
=>\(\dfrac{6-m^2+3m-2}{m-2}>=0\)
=>\(\dfrac{-m^2+3m+4}{m-2}>=0\)
=>\(\dfrac{m^2-3m-4}{m-2}< =0\)
=>\(\dfrac{\left(m-4\right)\left(m+1\right)}{m-2}< =0\)
Đặt \(F\left(x\right)=\dfrac{\left(m-4\right)\left(m+1\right)}{m-2}\)
Đặt m-4=0
=>m=4
Đặt m+1=0
=>m=-1
Đặt m-2=0
=>m=2
Ta có bảng xét dấu:
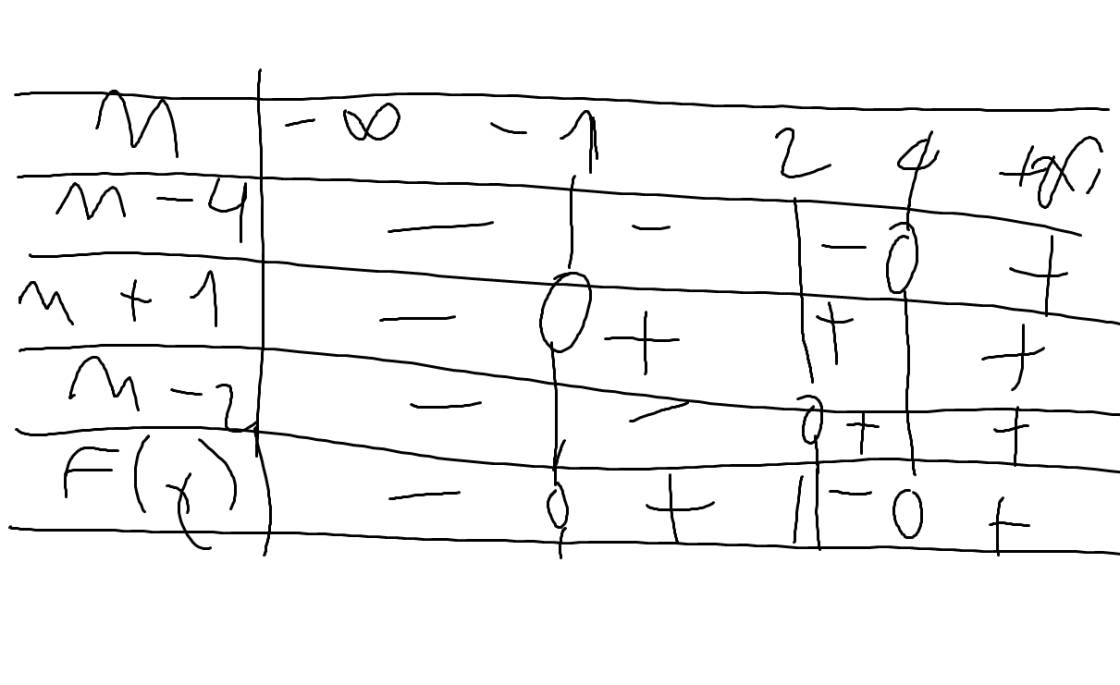
Theo BXD, ta có:F(x)<=0
=>\(\left[{}\begin{matrix}m< =-1\\2< m< =4\end{matrix}\right.\)