TN
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NL
1
AD
20 tháng 8 2023
Kẻ Az//Bx//Dy
=> BAD = BAz + DAz = (180o - ABx) + (180o - ADy) = 30o + 60o = 90o
20 tháng 8
Ta có: tia CD nằm giữa hai tia CF và CB
=>\(\hat{BCF}=\hat{BCD}+\hat{FCD}=20^0+50^0=70^0\)
Ta có: \(\hat{BCF}=\hat{ABC}\left(=70^0\right)\)
mà hai góc này là hai góc ở vị trí so le trong
nên AB//CF
Ta có: \(\hat{EDC}+\hat{DCF}=130^0+50^0=180^0\)
mà hai góc này là hai góc ở vị trí trong cùng phía
nên ED//CF
Ta có: AB//CF
ED//CF
Do đó: AB//DE
15 tháng 8
\(\frac{x}{10}=\frac{y}{5}\)
=>\(\frac{x}{2}=\frac{y}{1}\)
=>\(\frac{x}{4}=\frac{y}{2}\)
mà \(\frac{y}{2}=\frac{z}{3}\)
nên \(\frac{x}{4}=\frac{y}{2}=\frac{z}{3}\)
mà 2x-3y+4z=350
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\frac{x}{4}=\frac{y}{2}=\frac{z}{3}=\frac{2x-3y+4z}{2\cdot4-3\cdot2+4\cdot3}=\frac{350}{14}=25\)
=>\(\begin{cases}x=25\cdot4=100\\ y=25\cdot2=50\\ z=25\cdot3=75\end{cases}\)
20 tháng 8
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\frac{a+b-c}{c}=\frac{a+c-b}{b}=\frac{b+c-a}{a}=\frac{a+b-c+a+c-b+b+c-a}{a+b+c}=\frac{a+b+c}{a+b+c}=1\)
=>\(\begin{cases}a+b-c=c\\ a+c-b=b\\ b+c-a=a\end{cases}\Rightarrow\begin{cases}a+b=2c\\ a+c=2b\\ b+c=2a\end{cases}\)
\(A=\frac{\left(a+b\right)\left(b+c\right)\left(a+c\right)}{abc}=\frac{2a\cdot2b\cdot2c}{abc}=8\)
A
14 tháng 8
Bài giải:
Số tiền mỗi đơn vị đóng góp tỉ lệ thuận với số xe và tỉ lệ nghịch với khoảng cách, nên hệ số tỉ lệ của từng đơn vị là:
- Đơn vị 1: \(\frac{8}{1 , 5} = 5,33\)
- Đơn vị 2: \(\frac{5}{3} \approx 1,67\)
- Đơn vị 3: \(\frac{4}{1} = 4\)
Tổng hệ số: \(5,33 + 1,67 + 4 = 11\).
Vì tổng chi phí là \(340\) triệu đồng, mỗi đơn vị hệ số 1 sẽ trả \(\frac{340}{11} \approx 30,94\) triệu đồng.
Vậy:
- Đơn vị 1 trả: \(5,33 \times 30,94 \approx 164,85\) triệu đồng
- Đơn vị 2 trả: \(1,67 \times 30,94 \approx 51,52\) triệu đồng
- Đơn vị 3 trả: \(4 \times 30,94 \approx 123,64\) triệu đồng.
13 tháng 8
Gọi BM là tia đối của tia By
Ta có: \(\hat{ABy}+\hat{ABM}=180^0\) (hai góc kề bù)
=>\(\hat{ABM}=180^0-120^0=60^0\)
Ta có: tia BM nằm giữa hai tia BA và BC
=>\(\hat{ABM}+\hat{CBM}=\hat{ABC}\)
=>\(\hat{CBM}=90^0-60^0=30^0\)
Ta có: \(\hat{xAm}=\hat{ABM}\left(=60^0\right)\)
mà hai góc này là hai góc ở vị đồng vị
nên Ax//BM
=>Ax//By
Ta có: \(\hat{CBM}+\hat{BCz}=30^0+150^0=180^0\)
mà hai góc này là hai góc ở vị trí trong cùng phía
nên By//Cz
Ta có: Ax//By
By//Cz
Do đó: Ax//By//Cz
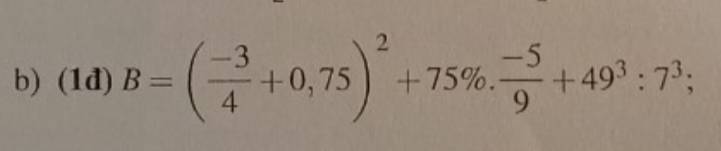
\(B=\left(-\dfrac{3}{4}+\dfrac{3}{4}\right)^2+\dfrac{3}{4}\cdot\dfrac{-5}{9}+7^3\)
=-15/36+343
=343-5/12=4111/12